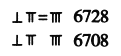题目内容
【题目】设函数![]() =
=![]() ,
,![]() 为
为![]() 的导函数.若
的导函数.若![]() 和
和![]() 的零点均在集合
的零点均在集合![]() 中,则
中,则![]() ( )
( )
A.在![]() 上单调递增B.在
上单调递增B.在![]() 上单调递增
上单调递增
C.极小值为![]() D.最大值为
D.最大值为![]()
【答案】B
【解析】
依题意,可求得![]() 和
和![]() 的零点构成的集合为
的零点构成的集合为![]() ,
,![]() ,
,![]() ,0,
,0,![]() ,分6类讨论,可确定
,分6类讨论,可确定![]() 、
、![]() 的值,继而利用导数确定函数的极值及单调区间,从而判断四个选项,可得答案.
的值,继而利用导数确定函数的极值及单调区间,从而判断四个选项,可得答案.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
令![]() 得:
得:![]() 或
或![]() ;
;
令![]() 得:
得:![]() ,或
,或![]() ;
;
由![]() 知,
知,![]() 和
和![]() 的零点构成的集合为
的零点构成的集合为![]() ,
,![]() ,
,![]() ,
,
又![]() 和
和![]() 的零点均在集合
的零点均在集合![]() ,0,
,0,![]() 中,
中,
①若![]() ,
,![]() ,则
,则![]() ,不符合题意,舍去;
,不符合题意,舍去;
②若![]() ,
,![]() ,则
,则![]() ,不符合题意,舍去;
,不符合题意,舍去;
③若![]() ,
,![]() ,则
,则![]() ,不符合题意,舍去;
,不符合题意,舍去;
④若![]() ,
,![]() ,则
,则![]() ,不符合题意,舍去;
,不符合题意,舍去;
⑤若![]() ,
,![]() ,则
,则![]() ,不符合题意,舍去;
,不符合题意,舍去;
⑥若![]() ,
,![]() ,则
,则![]() ,符合题意;
,符合题意;
故![]() ,
,
令![]() ,得:
,得:![]() 或
或![]() ;
;
![]() ,得:
,得:![]() ;
;
![]() 为极小值点,
为极小值点,![]() ,排除C;
,排除C;
![]() 为极大值点,
为极大值点,![]() ,当
,当![]() 时,
时,![]() ,排除D;
,排除D;
![]() 在区间
在区间![]() 上单调递减,排除A;
上单调递减,排除A;
在![]() ,
,![]() 单调递增,
单调递增,![]() ,
,![]() ,
,
故B在![]() 上单调递增,B正确;
上单调递增,B正确;
故选:B.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】已知某种新型病毒的传染能力很强,给人们生产和生活带来很大的影响,所以创新研发疫苗成了当务之急.为此,某药企加大了研发投入,市场上这种新型冠状病毒的疫苗![]() 的研发费用
的研发费用![]() (百万元)和销量
(百万元)和销量![]() (万盒)的统计数据如下:
(万盒)的统计数据如下:
研发费用 | 2 | 3 | 6 | 10 | 13 | 14 |
销量 | 1 | 1 | 2 | 2.5 | 4 | 4.5 |
(1)根据上表中的数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (用分数表示);
(用分数表示);
(2)根据所求的回归方程,估计当研发费用为1600万元时,销售量为多少?
参考公式: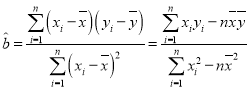 ,
,![]() .
.
【题目】某保险公司给年龄在![]() 岁的民众提供某种疾病的一年期医疗保险,现从
岁的民众提供某种疾病的一年期医疗保险,现从![]() 名参保人员中随机抽取
名参保人员中随机抽取![]() 名作为样本进行分析,按年龄段
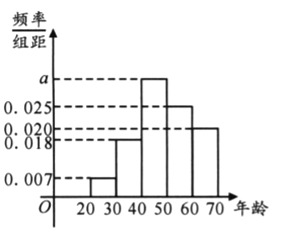
名作为样本进行分析,按年龄段![]() 分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
年龄 (单位:岁) |
|
|
|
|
|
保费 (单位:元) |
|
|
|
|
|
(1)用样本的频率分布估计总体分布,为使公司不亏本,求![]() 精确到整数时的最小值
精确到整数时的最小值![]() ;
;
(2)经调查,年龄在![]() 之间老人每
之间老人每![]() 人中有
人中有![]() 人患该项疾病(以此频率作为概率).该病的治疗费为
人患该项疾病(以此频率作为概率).该病的治疗费为![]() 元,如果参保,保险公司补贴治疗费
元,如果参保,保险公司补贴治疗费![]() 元.某老人年龄
元.某老人年龄![]() 岁,若购买该项保险(
岁,若购买该项保险(![]() 取
取![]() 中的
中的![]() ).针对此疾病所支付的费用为
).针对此疾病所支付的费用为![]() 元;若没有购买该项保险,针对此疾病所支付的费用为
元;若没有购买该项保险,针对此疾病所支付的费用为![]() 元.试比较
元.试比较![]() 和
和![]() 的期望值大小,并判断该老人购买此项保险是否划算?
的期望值大小,并判断该老人购买此项保险是否划算?
【题目】算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大贡献.在算筹记数法中,以“纵式”和“横式”两种方式来表示数字,如下表:
数字形式 |
|
|
|
|
|
|
|
|
|
纵式 |
|
|
|
|
|
|
|
|
|
横式 |
|
|
|
|
|
|
|
|
|
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如图所示.如果把![]() 根算筹以适当的方式全部放入下面的表格中,那么可以表示的三位数的个数为______.
根算筹以适当的方式全部放入下面的表格中,那么可以表示的三位数的个数为______.