题目内容
【题目】平面直角坐标系xOy中,已知椭圆![]() 的离心率为
的离心率为![]() ,左右焦点分别是
,左右焦点分别是![]() 和
和![]() ,以
,以![]() 为圆心,3为半径的圆与以
为圆心,3为半径的圆与以![]() 为圆心,1为半径的圆相交,且交点在椭圆C上.
为圆心,1为半径的圆相交,且交点在椭圆C上.
(1)求椭圆C的方程.
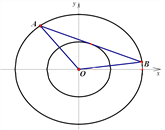
(2)设椭圆![]() ,P为椭圆C上任意一点,过点P的直线
,P为椭圆C上任意一点,过点P的直线![]() 交椭圆E于A、B两点,射线OP交椭圆E于点Q.
交椭圆E于A、B两点,射线OP交椭圆E于点Q.
①判断![]() 是否为定值?若是定值求出该定值,若不是定值说明理由.
是否为定值?若是定值求出该定值,若不是定值说明理由.
②求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)①
;(2)①![]() 为定值,定值为2;②
为定值,定值为2;②![]() .
.
【解析】
(1) 设两圆的一个交点为P,则![]() ,
,![]() ,由椭圆的定义可求出
,由椭圆的定义可求出![]() ,又离心率为
,又离心率为![]() 求出
求出![]() ,从而可得椭圆C的方程;
,从而可得椭圆C的方程;
(2) ①设P(x0,y0),![]() ,可得
,可得![]() ,将其代入椭圆
,将其代入椭圆![]() 的方程可得结果;
的方程可得结果;
②设A(x1,y1),B(x2,y2),将直线![]() 与椭圆E的方程联立,利用根与系数的关系表示出弦长
与椭圆E的方程联立,利用根与系数的关系表示出弦长![]() ,同时直线与两椭圆都有交点,两个判别式大于0,
,同时直线与两椭圆都有交点,两个判别式大于0,![]() 到直线的距离将
到直线的距离将![]() 到直线
到直线![]() 的距离
的距离![]() 表示出来,再将面积表示出来求最值可求得结果.
表示出来,再将面积表示出来求最值可求得结果.
(1)设两圆的一个交点为P,则![]() ,
,![]() ,
,
由P在椭圆上可得![]() ,
,
则![]() ,
,![]() ,得
,得![]() ,则
,则![]() ,
,
故椭圆方程为![]() .
.
(2)①椭圆![]() 方程
方程![]() ,
,![]() ,则
,则![]() ,
,
![]() 在射线
在射线![]() 上,
上,![]() ,
,![]()
![]() ,
,
代入![]() 可得
可得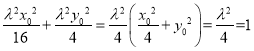 ,
,
![]() ,
,![]() =2.
=2.
②直线为![]() ,由①可得
,由①可得![]() 为
为![]() 的中点,
的中点,![]() 在直线上,
在直线上,
则![]() 到直线的距离与
到直线的距离与![]() 到直线的距离相等,则
到直线的距离相等,则![]() ,
,
![]() ,
,![]() ,联立
,联立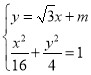 ,
,![]() ,
,
则![]() ,
,![]() ,
,
![]() =
=![]() ,
,
联立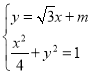 ,得
,得![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
![]() ,当
,当![]() 时,
时,![]() 面积的最大值为
面积的最大值为![]() .
.

 阅读快车系列答案
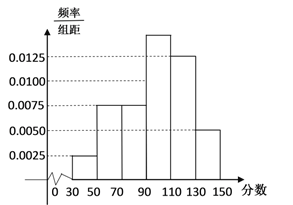
阅读快车系列答案【题目】某高中数学建模兴趣小组的同学为了研究所在地区男高中生的身高与体重的关系,从若干个高中男学生中抽取了1000个样本,得到如下数据.
数据一:身高在![]() (单位:
(单位:![]() )的体重频数统计
)的体重频数统计
体重 ( |
|
|
|
|
|
|
|
|
人数 | 20 | 60 | 100 | 100 | 80 | 20 | 10 | 10 |
数据二:身高所在的区间含样本的个数及部分数据
身高 |
|
|
|
|
|
平均体重
| 45 | 53.6 | 60 | 75 |
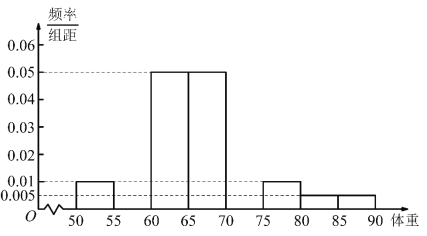
(1)依据数据一将上面男高中生身高在![]() (单位:
(单位:![]() )体重的频率分布直方图补充完整,并利用频率分布直方图估计身高在
)体重的频率分布直方图补充完整,并利用频率分布直方图估计身高在![]() (单位:
(单位:![]() )的中学生的平均体重;(保留小数点后一位)
)的中学生的平均体重;(保留小数点后一位)
(2)依据数据一、二,计算身高(取值为区间中点)和体重的相关系数约为0.99,能否用线性回归直线来刻画中学生身高与体重的相关关系,请说明理由;若能,求出该回归直线方程;
(3)说明残差平方和或相关指数![]() 与线性回归模型拟合效果之间关系.(只需写出结论,不需要计算)
与线性回归模型拟合效果之间关系.(只需写出结论,不需要计算)
参考公式: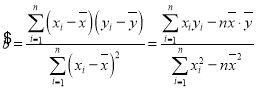 ,
,![]() .
.
参考数据:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ;(4)
;(4)![]() .
.