题目内容
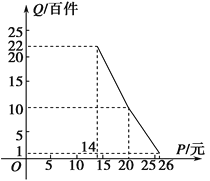
【题目】某人为研究中学生的性别与每周课外阅读量这两个变量的关系,随机抽查了100名中学生,得到频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].

(Ⅰ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生周课外阅读时间的平均数.
(Ⅱ)在样本数据中,有20位女生的每周课外阅读时间超过4小时,15位男生的每周课外阅读时间没有超过4小时.请画出每周课外阅读时间与性别列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“该校学生的每周课外阅读时间与性别有关”.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附: 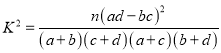
【答案】(Ⅰ)5.8;(Ⅱ)答案见解析.
【解析】试题分析:(1)根据频率分布直方图计算100名学生周课外阅读时间的平均数;(2)计算![]() 的值,结合独立性检验的结论即可得到结果.
的值,结合独立性检验的结论即可得到结果.
试题解析:
(Ⅰ)由频率分布直方图得
![]() =1×0.05+3×0.2+5×0.3+7×0.25+9×0.15+11×0.05=5.8.
=1×0.05+3×0.2+5×0.3+7×0.25+9×0.15+11×0.05=5.8.
(Ⅱ)由(Ⅰ)知,100位学生中有100×0.75=75(位)的每周课外阅读时间超过4小时, 25人的每周课外阅读时间不超过4小时.所以每周课外阅读时间与性别列联表如下:
男生 | 女生 | 总计 | |
每周课外阅读时间不超过4小时 | 15 | 10 | 25 |
每周课外阅读时间超过4小时 | 55 | 20 | 75 |
总计 | 70 | 30 | 100 |
结合列联表可算得K2的观测值k=![]() =
=![]() ≈1.59<3.841.
≈1.59<3.841.
所以不能在犯错误的概率不超过0.05的前提下认为“该校学生的每周课外阅读时间与性别有关”.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目