题目内容
已知圆 与圆
与圆 相交,则圆
相交,则圆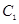 与圆
与圆 的公共弦所在的直线的方程为( )
的公共弦所在的直线的方程为( )
A. | B. |
C. | D. |
B
解析试题分析:∵ ,
, ,∴两圆的公共弦所在直线方程为x+2y-1=0,
,∴两圆的公共弦所在直线方程为x+2y-1=0,
考点:本题考查了圆与圆的位置关系
点评:两圆相减即可得到两圆公共弦所在的直线方程

练习册系列答案
相关题目
若过定点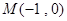 且斜率为
且斜率为 的直线与圆
的直线与圆 在第一象限内的部分有交点,则
在第一象限内的部分有交点,则 的取值范围是( ).
的取值范围是( ).
A. | B.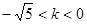 |
C. | D. |
圆 :
: 与圆
与圆 :
: 的位置关系是( )
的位置关系是( )
| A.相交 | B.外切 | C.内切 | D.相离 |
若方程 表示一个圆,则有( )
表示一个圆,则有( )
A. | B.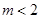 | C. | D. |
一束光线从点 出发经
出发经 轴反射,到达圆C:
轴反射,到达圆C: 上一点的最短路程是( )
上一点的最短路程是( )
| A.4 | B.5 |
C.3 -1 -1 | D.2 |
以两点 和
和 为直径端点的圆的方程是
为直径端点的圆的方程是
A. | B. |
C. | D. |
若圆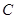 的半径为1,圆心在第一象限,且与直线
的半径为1,圆心在第一象限,且与直线 和
和 轴相切,则该圆的标准方程是 ( )
轴相切,则该圆的标准方程是 ( )
A. | B. |
C. | D. |
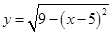 的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是( )
的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是( )



 ,则直线倾斜角的取值范围是( )
,则直线倾斜角的取值范围是( )


