题目内容
一束光线从点 出发经
出发经 轴反射,到达圆C:
轴反射,到达圆C: 上一点的最短路程是( )
上一点的最短路程是( )
| A.4 | B.5 |
C.3 -1 -1 | D.2 |
A
解析试题分析:对于研究距离的最值问题,一般运用等价转换的思想,转化到一条直线上,利用三边的不等式关系得到。求解A到入射点的距离加上入射点到圆上点的距离和的最小值,转化为点A关于x轴的对称点到入射点的距离加上入射点到圆上点的距离和的最小值即可。
因为点A的关于x轴的对称点(-1,-1),圆心坐标为(2,3),则这两点之间的距离为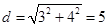 ,而圆的半径为1,可知最小的距离为5-1=4.故选A
,而圆的半径为1,可知最小的距离为5-1=4.故选A
考点:本试题考查了光的反射原理与直线与圆的位置关系的运用。
点评:解决该试题中的距离的最小值问题,要运用物理中的光线的反射原理,先求点A的关于x轴的对称点B,那么点B与圆心的连线减去圆的半径即为所求。

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
圆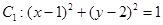 ,圆
,圆 ,则这两圆公切线的条数
,则这两圆公切线的条数
为 ( )
| A.1 | B.2 | C.3 | D.4 |
在平面直角坐标系 中,直线
中,直线 与圆
与圆 相交于
相交于 两点,则弦
两点,则弦 的长等于( )
的长等于( )
A. | B. | C.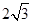 | D.1 |
已知圆 与圆
与圆 相交,则圆
相交,则圆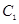 与圆
与圆 的公共弦所在的直线的方程为( )
的公共弦所在的直线的方程为( )
A. | B. |
C. | D. |
若圆 上有且只有两个点到直线
上有且只有两个点到直线 的距离等于
的距离等于 ,则半径
,则半径 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知 ,则函数
,则函数 的零点个数为
的零点个数为
| A.1 | B.2 | C.3 | D.4 |
圆 和
和 的位置关系为( )
的位置关系为( )
| A.外切 | B.内切 | C.外离 | D.内含 |
圆x2+y2-4x+4y+6=0截直线x-y-5=0所得的弦长等于( )
A. | B. | C.1 | D.5 |
 所表示的曲线的图形是( )
所表示的曲线的图形是( )