Question

【题目】已知函数.

（1）求函数的单调区间；

（2）设函数.当时，若函数在上为增函数，求实数的取值范围.

Answer 1

【答案】(1) 在上单调递减，在，上单调递增.

(2) .

【解析】

（1）求导，根据正负讨论导函数符号，确定对应单调区间，（2）先利用导数研究正负，根据正负去绝对值将化为分段函数，再利用导数分段研究单调性，利用变量分离法转化为求对应函数最值问题，最后根据最值确定实数的取值范围.

（1）对求导得

（i）若，当时，，当或时，

所以在上单调递增，在，上单调递减

（ii）若，当时，，当或时，

所以在上单调递减，在，上单调递增.

（2）记函数，

考察函数的符号

对函数求导得

当时，恒成立

当时，

从而

∴在上恒成立，故在上单调递减.

∴

∴

又曲线在上连续不间断，所以由函数的零点存在性定理及其单调性知

存在唯一的，使，

所以当时，，当时，

∴，∴

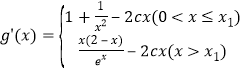
由上述讨论过程可知曲线在上连续不断，又函数为增函数

所以在上恒成立

①当时，在上恒成立，即在上恒成立，

记 ，，则，

当变化时，，变化情况如下表：

∴

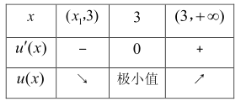
故“在上恒成立”只需，即

②当时，，

当时，在上恒成立

综合①②，知当时，函数在为增函数

故实数的取值范围是.