题目内容
(12分)
如图,直角梯形ABCD,∠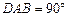 ,AD∥BC,AB=2,AD=
,AD∥BC,AB=2,AD=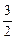 ,BC=
,BC=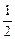 椭圆F以A、B为焦点且过点D,
椭圆F以A、B为焦点且过点D,

(Ⅰ)建立适当的直角坐标系,求椭圆的方程;
( Ⅱ)若点E满足
Ⅱ)若点E满足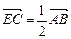 ,是否存在斜率
,是否存在斜率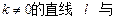
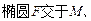
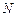 两点,且
两点,且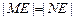 ,若存在,求K的取值范围;若不存在,说明理由。
,若存在,求K的取值范围;若不存在,说明理由。
如图,直角梯形ABCD,∠
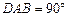 ,AD∥BC,AB=2,AD=
,AD∥BC,AB=2,AD=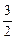 ,BC=
,BC=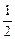 椭圆F以A、B为焦点且过点D,
椭圆F以A、B为焦点且过点D,
(Ⅰ)建立适当的直角坐标系,求椭圆的方程;
(
 Ⅱ)若点E满足
Ⅱ)若点E满足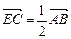 ,是否存在斜率
,是否存在斜率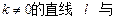
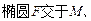
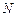 两点,且
两点,且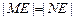 ,若存在,求K的取值范围;若不存在,说明理由。
,若存在,求K的取值范围;若不存在,说明理由。(Ⅰ)以AB中点为原点O,AB所在直线为x轴,建立直角坐标系,如图
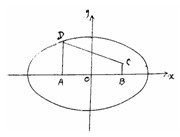
则A(-1,0) B(1,0) D(-1,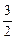 )
)
设椭圆F的方程为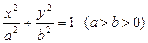
得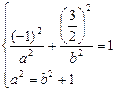
得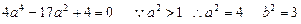
所求椭圆F方程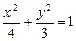
(Ⅱ)由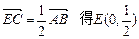
显然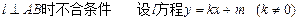
代入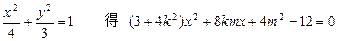
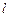 与椭圆F有两不同公共点的充要条件是
与椭圆F有两不同公共点的充要条件是
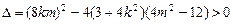

即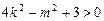
设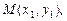

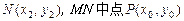
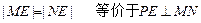
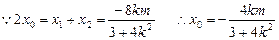
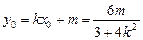

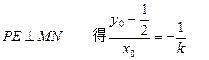
得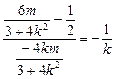 得
得 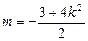
代入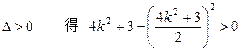
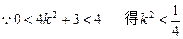
又
解法2, 设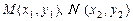
得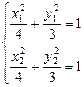
①—② 得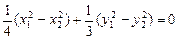
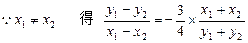
设
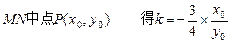 得
得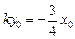 ③
③
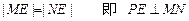
得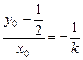 得
得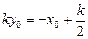 ④
④
由③、④得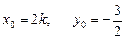
且P(x0,y0)在椭圆F内部
得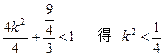
又

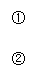

则A(-1,0) B(1,0) D(-1,
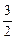 )
) 设椭圆F的方程为
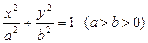
得
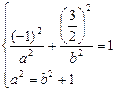
得
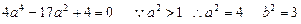
所求椭圆F方程
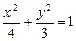
(Ⅱ)由
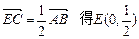
显然
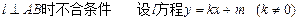
代入
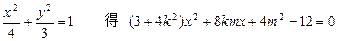
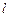 与椭圆F有两不同公共点的充要条件是
与椭圆F有两不同公共点的充要条件是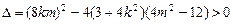

即
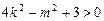
设
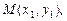

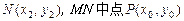
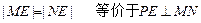
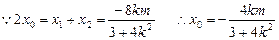
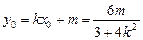

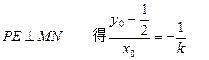
得
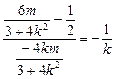 得
得 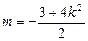
代入
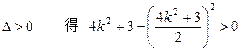
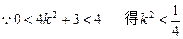
又

解法2, 设
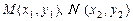
得
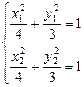
①—② 得
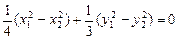
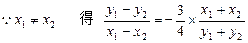
设

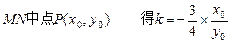 得
得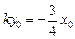 ③
③ 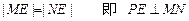
得
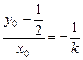 得
得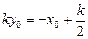 ④
④ 由③、④得
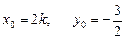
且P(x0,y0)在椭圆F内部
得
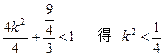
又


略

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
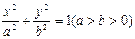 的焦点分别为
的焦点分别为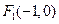 、
、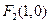 ,直线
,直线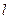 :
: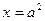 交
交 轴于点
轴于点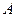 ,且
,且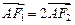 .
.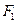 、
、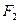 分别作互相垂直的两直线与椭圆分别 交于
分别作互相垂直的两直线与椭圆分别 交于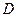 、
、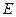 、
、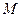 、
、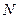 四点(如图所示),试求四边形
四点(如图所示),试求四边形 面积的最大值和最小值.
面积的最大值和最小值.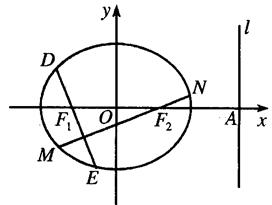
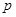 是椭圆
是椭圆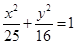 上的点.若
上的点.若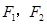 是椭圆的两个焦点,则
是椭圆的两个焦点,则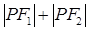 等于( )
等于( )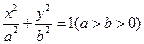 的左、右焦点为
的左、右焦点为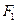 、
、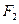 ,离心率为
,离心率为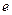 。直线
。直线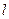 :
: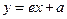 与
与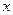 轴、
轴、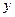 轴分别交于点A、B,M是直线
轴分别交于点A、B,M是直线 椭圆C的一个公共点,P是点
椭圆C的一个公共点,P是点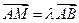 。
。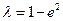
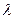 的值,使得
的值,使得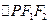 是等腰三角形。
是等腰三角形。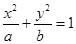 和直线
和直线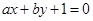 (
( 为非零实数)在同一坐标系中,它们的图形可能是( )
为非零实数)在同一坐标系中,它们的图形可能是( )
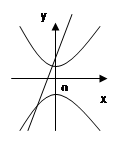

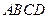 中,
中,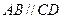 ,且
,且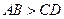 。设以
。设以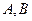 为焦点且过点
为焦点且过点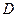 的双曲线的离心率为
的双曲线的离心率为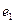 ,以
,以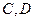 为焦点且过点
为焦点且过点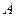 的椭圆的离心率为
的椭圆的离心率为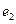 ,则
,则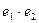 = ;
= ;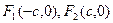 为椭圆
为椭圆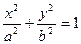 的两个焦点,P为椭圆上一点且
的两个焦点,P为椭圆上一点且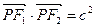 ,则此椭圆离心率的取值范围是 ( ▲ )
,则此椭圆离心率的取值范围是 ( ▲ )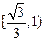

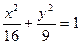 的焦距是 ,焦点坐标为 ;若CD为过左焦点
的焦距是 ,焦点坐标为 ;若CD为过左焦点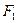 的弦,则
的弦,则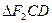 的周长为
的周长为