题目内容
【题目】如图,在四棱锥![]() 中,底而
中,底而![]() 为菱形,且菱形
为菱形,且菱形![]() 所在的平面与
所在的平面与![]() 所在的平面相互垂直,
所在的平面相互垂直,![]() ,
,![]() ,
,![]() ,
,![]() .
.
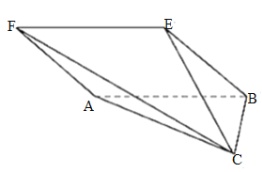
(1)求证:![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的最长侧棱的长.
的最长侧棱的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)在菱形![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,由此可证.
,由此可证.
(2)取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,由已知易得:
,由已知易得:![]() 是正三角形,
是正三角形,![]() ,进一步可证
,进一步可证![]() 平面
平面![]() ,由勾股定理可求出侧棱
,由勾股定理可求出侧棱![]() ,
,![]() ,
,![]() ,
,![]() 的长度,得到最长的是
的长度,得到最长的是![]() ,或可先判断CF最长,求解出长度即可.
,或可先判断CF最长,求解出长度即可.
(1)在菱形![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() .
.
(2)方法一:取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,
,
由已知易得:![]() 是正三角形,∴
是正三角形,∴![]() .
.
又∴平面![]() 平面
平面![]() 且交线为
且交线为![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,![]() ,
,
在菱形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
显然在侧棱![]() ,
,![]() ,
,![]() ,
,![]() 中最长的是
中最长的是![]() .
.
∴四棱锥![]() 的最长侧棱的长为
的最长侧棱的长为![]() .
.
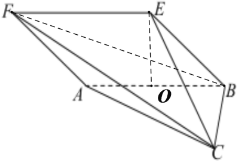
方法二:取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,
,
由已知易得:![]() 是正三角形,∴
是正三角形,∴![]() ,
,
又∵平面![]() 平面
平面![]() 且交线为
且交线为![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() ,
,![]() 平面
平面![]() ∴
∴![]() ,
,![]() .
.
在菱形![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() 最长.
最长.
在![]() 中,
中,![]() .
.
∴四棱锥![]() 的最长侧棱的长为
的最长侧棱的长为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某地自2014年至2019年每年年初统计所得的人口数量如表所示:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人数(单位:千人) | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)根据表中的数据判断从2014年到2019年哪个跨年度的人口增长数量最大?并描述该地人口数量的变化趋势;
(2)研究人员用函数![]() 拟合该地的人口数量,其中
拟合该地的人口数量,其中![]() 的单位是年,2014年年初对应时刻
的单位是年,2014年年初对应时刻![]() ,
,![]() 的单位是千人,经计算可得
的单位是千人,经计算可得![]() ,请解释
,请解释![]() 的实际意义.
的实际意义.
【题目】“绿水青山就是金山银山”,为了响应国家政策,我市环保部门对市民进行了一次环境保护知识的网络问卷调查,每位市民仅有一次参加机会,通过随机抽样,得到参与问卷调查的50人的得分(满分:100分)数据,统计结果如表所示:
组别 |
|
|
|
|
|
|
男 | 1 | 2 | 2 | 10 | 9 | 6 |
女 | 0 | 5 | 5 | 5 | 3 | 2 |
若规定问卷得分不低于70分的市民称为“环境保护关注者”,则上图中表格可得![]() 列联表如下:
列联表如下:
非“环境保护关注者” | 是“环境保护关注者” | 合计 | |
男 | 5 | 25 | 30 |
女 | 10 | 10 | 20 |
合计 | 15 | 35 | 50 |
(1)请完成上述![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“环境保护关注者”与性别有关?
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“环境保护关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“环境保护达人”,现在从本次调查的“环境保护达人”中利用分层抽样的方法抽取4名市民参与环保知识问答,再从这4名市民中随机抽取2人参与座谈会,求抽取的2名市民中,既有男“环境保护达人”又有女“环境保护达人”的概率.
附表及公式: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】推进垃圾分类处理,是落实绿色发展理念的必然选择,也是打赢污染防治攻坚战的重要环节.为了解居民对垃圾分类的了解程度,某社区居委会随机抽取1000名社区居民参与问卷测试,并将问卷得分绘制频率分布表如下:
得分 |
|
|
|
|
|
|
|
男性人数 | 40 | 90 | 120 | 130 | 110 | 60 | 30 |
女性人数 | 20 | 50 | 80 | 110 | 100 | 40 | 20 |
(1)从该社区随机抽取一名居民参与问卷测试,试估计其得分不低于60分的概率;
(2)将居民对垃圾分类的了解程度分为“比较了解“(得分不低于60分)和“不太了解”(得分低于60分)两类,完成![]() 列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关?
列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关?
不太了解 | 比较了解 | |
男性 | ||
女性 |
(3)从参与问卷测试且得分不低于80分的居民中,按照性别进行分层抽样,共抽取10人,连同![]() 名男性调查员一起组成3个环保宜传队.若从这
名男性调查员一起组成3个环保宜传队.若从这![]() 中随机抽取3人作为队长,且男性队长人数占的期望不小于2.求
中随机抽取3人作为队长,且男性队长人数占的期望不小于2.求![]() 的最小值.
的最小值.
附:![]()
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |