题目内容
 如图所示,某几何体的正视图、侧视图均为等腰三角形,俯视图是正方形,则该几何体的外接球的体积是
如图所示,某几何体的正视图、侧视图均为等腰三角形,俯视图是正方形,则该几何体的外接球的体积是分析:此几何体是四棱锥,由图形其高与底面边长已知,由此判断知,球心正好是底面中心,故球半径易求答案.
解答:解:由三视图知,此几何体是一个高为
,底面边长为2的正方体,顶点在底面上的投影是底面的中心,用此中心到五个顶点的距离都是
故此中心即是几何体外接球的球心,故球的半径让车
故其外接球的体积是
π(
)3=
π
故答案为
π
| 2 |
| 2 |
故此中心即是几何体外接球的球心,故球的半径让车
| 2 |
故其外接球的体积是
| 4 |
| 3 |
| 2 |
8
| ||
| 3 |
故答案为
8
| ||
| 3 |
点评:本题考查由三视图复原实物图的能力,以及根据其几何特征求其外接球的半径的能力,球与其内接多面体的几何特征的转换是立体几何中考查的一个重点,注意总结其规律.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
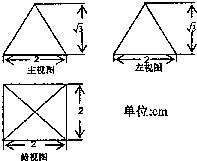 如图所示,某几何体的主视图、左视图均是等腰三角形,俯视图是正方形,则该几何体的全面积(单位:cm3)为( )
如图所示,某几何体的主视图、左视图均是等腰三角形,俯视图是正方形,则该几何体的全面积(单位:cm3)为( )A、4+4
| ||
| B、12 | ||
C、4+8
| ||
| D、20 |
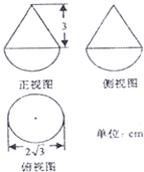 如图所示,某几何体的正视图、侧视图均为半圆和等边三角形的组合,俯视图为圆形,则该几何体的全面积为
如图所示,某几何体的正视图、侧视图均为半圆和等边三角形的组合,俯视图为圆形,则该几何体的全面积为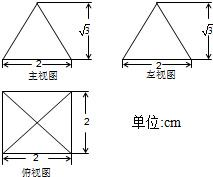 如图所示,某几何体的主视图、左视图均是等腰三角形,俯视图是正方形.则该几何体的全面积为
如图所示,某几何体的主视图、左视图均是等腰三角形,俯视图是正方形.则该几何体的全面积为 如图所示为某几何体的直观图和三视图,上半部分是四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.
如图所示为某几何体的直观图和三视图,上半部分是四棱锥P-EFGH,下半部分是长方体ABCD-EFGH. (2011•许昌三模)如图所示为某几何体的三视图,均是直角边长为1的等腰直角三角形,则此几何体的表面积是( )
(2011•许昌三模)如图所示为某几何体的三视图,均是直角边长为1的等腰直角三角形,则此几何体的表面积是( )