题目内容
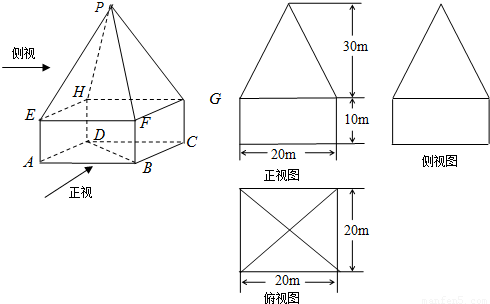
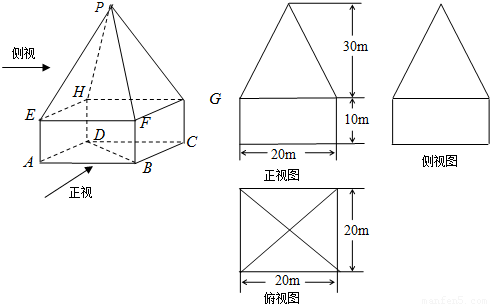
 如图所示为某几何体的直观图和三视图,上半部分是四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.
如图所示为某几何体的直观图和三视图,上半部分是四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.(1)求该几何体的体积;
(2)证明:直线BD⊥平面PEG.
分析:(1)由题意知该几何体的体积V=VP-EFGH+VABCD-EFGH,由此能求出该几何体的体积.
(2)连接EG,HF,BD,EG∩HF=O,连接PO,由正四棱锥的性质知:PO⊥平面EFGH,故PO⊥HF,所以HF⊥平面PEG,再由BD∥HF,能够证明BD⊥平面PEG.
(2)连接EG,HF,BD,EG∩HF=O,连接PO,由正四棱锥的性质知:PO⊥平面EFGH,故PO⊥HF,所以HF⊥平面PEG,再由BD∥HF,能够证明BD⊥平面PEG.
解答:解:(1)由题意知该几何体的体积
V=VP-EFGH+VABCD-EFGH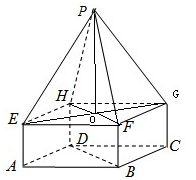
=
×202×30+202×10
=8000(m2).
(2)如图,连接EG,HF,BD,EG∩HF=O,
连接PO,由正四棱锥的性质知:
PO⊥平面EFGH,∴PO⊥HF,
又∵EG⊥HF,∴HF⊥平面PEG,
又∵BD∥HF,∴BD⊥平面PEG.
V=VP-EFGH+VABCD-EFGH

=
| 1 |
| 3 |
=8000(m2).
(2)如图,连接EG,HF,BD,EG∩HF=O,
连接PO,由正四棱锥的性质知:
PO⊥平面EFGH,∴PO⊥HF,
又∵EG⊥HF,∴HF⊥平面PEG,
又∵BD∥HF,∴BD⊥平面PEG.
点评:本题考查几何体的体积的求法,考查直线与平面垂直的证明.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
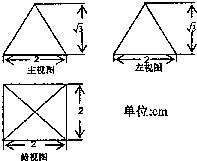 如图所示,某几何体的主视图、左视图均是等腰三角形,俯视图是正方形,则该几何体的全面积(单位:cm3)为( )
如图所示,某几何体的主视图、左视图均是等腰三角形,俯视图是正方形,则该几何体的全面积(单位:cm3)为( )A、4+4
| ||
| B、12 | ||
C、4+8
| ||
| D、20 |
 (2011•许昌三模)如图所示为某几何体的三视图,均是直角边长为1的等腰直角三角形,则此几何体的表面积是( )
(2011•许昌三模)如图所示为某几何体的三视图,均是直角边长为1的等腰直角三角形,则此几何体的表面积是( )