题目内容
【题目】设f（k）是满足不等式log2x+log2（52k﹣1﹣x）≥2k（k∈N*）的自然数x的个数．
（1）求f（k）的函数解析式；
（2）Sn=f（1）+2f（2）+…+nf（n），求Sn ．
【答案】
（1）
解：由原不等式得log2（52k﹣1x﹣x2）≥2k=log222k，
则x2﹣52k﹣1x+22k≤0，
故2k﹣1≤x≤42k﹣1．
∴f（k）=42k﹣1﹣2k﹣1+1=32k﹣1+1（k∈N*）；
（2）
解：kf（k）=3k2k﹣1+k．
Sn=f（1）+2f（2）+…+nf（n）=3（1+22+…+n2n﹣1）+（1+2+…+n），
设t=1+22+…+n2n﹣1（1）
2t=12+222+…+n2n（2）
（1）式减（2）式得﹣t=1+2+…+2n﹣1﹣n2n
∴t=（n﹣1）2n+1
∴ 
．
【解析】（1）由原不等式得log2（52k﹣1x﹣x2）≥2k=log222k ， 则x2﹣52k﹣1x+22k≤0，得到x的取值范围后，就能求出f（k）的解析式；（2）由Sn=f（1）+2f（2）+…+nf（n）=3（1+22+…+n2n﹣1）+（1+2+…+n），利用错位相减法、等差数列的求和公式，即可求得结果．
【考点精析】本题主要考查了对数的运算性质和数列的前n项和的相关知识点，需要掌握①加法：
②减法：
③数乘：
④
⑤
；数列{an}的前n项和sn与通项an的关系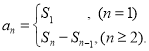
才能正确解答此题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
【题目】有一个容量为60的样本（60名学生的数学考试成绩），分组情况如表：
分组 | 0.5～20.5 | 20.5～40.5 | 40.5～60.5 | 60.5～80.5 | 80.5～100.5 |
频数 | 3 | 6 | 12 | ||
频率 | 0.3 |
（1）填出表中所剩的空格；
（2）画出频率分布直方图．
