题目内容
【题目】已知点P(1,1),过点P动直线l与圆C:x2+y2﹣2y﹣4=0交与点A,B两点.
(1)若|AB|= ![]() ,求直线l的倾斜角;
,求直线l的倾斜角;
(2)求线段AB中点M的轨迹方程.
【答案】
(1)解:由题意:圆C:x2+y2﹣2y﹣4=0,
化为圆的标准方程x2+(y﹣1)2=5,圆心C(0,1),r= ![]() .
.
∵又|AB|= ![]()
当动直线l的斜率不存在时,直线l的方程为x=1时,显然不满足题意;
当动直线l的斜率存在时,设动直线l的方程为:y﹣1=k(x﹣1)即kx﹣y+1﹣k=0
故弦心距d= ![]() =
= ![]() .
.
再由点到直线的距离公式可得d= ![]() =
= ![]() ,
,
解得:k=± ![]() .
.
即直线l的斜率等于± ![]() ,
,
根据tanθ=k,
故得直线l的倾斜角等于 ![]() 或
或 ![]() .
.
(2)解:由题意:线段AB中点为M,设M的坐标(x,y),
由垂径定理可知∠PMC=90°,故点M的轨迹是以CP为直径的圆,
又∵点C(0,1),P(1,1)
故M的轨迹方程为 ![]() .
.
【解析】(1)利用点斜式,设出过P点的直线l,利用与圆的弦长为 ![]() ,求出k的值,可得直线l的倾斜角;(2)设M的坐标(x,y),由垂径定理可知∠PMC=90°,故点M的轨迹是以CP为直径的圆.可得方程.
,求出k的值,可得直线l的倾斜角;(2)设M的坐标(x,y),由垂径定理可知∠PMC=90°,故点M的轨迹是以CP为直径的圆.可得方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数![]() (份)与收入
(份)与收入![]() (元)之间有如下的对应数据:
(元)之间有如下的对应数据:
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
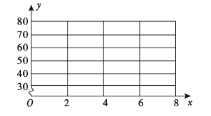
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式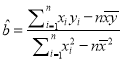 ,
, ![]() ;
;
②参考数据: ![]() ,
, ![]() ,
, ![]() .
.