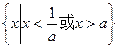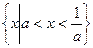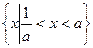题目内容
已知二次函数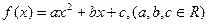 满足:对任意实数x,都有
满足:对任意实数x,都有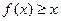 ,且当
,且当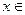 (1,3)时,有
(1,3)时,有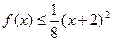 成立。
成立。
(1)证明: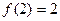 ;
;
(2)若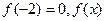 的表达式;
的表达式;
(3)设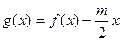 ,
,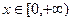 ,若
,若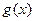 图上的点都位于直线
图上的点都位于直线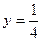 的上方,求
的上方,求
实数m的取值范围。
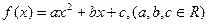 满足:对任意实数x,都有
满足:对任意实数x,都有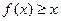 ,且当
,且当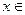 (1,3)时,有
(1,3)时,有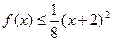 成立。
成立。(1)证明:
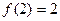 ;
;(2)若
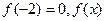 的表达式;
的表达式;(3)设
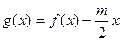 ,
,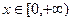 ,若
,若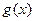 图上的点都位于直线
图上的点都位于直线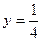 的上方,求
的上方,求实数m的取值范围。
(1)证明略(2)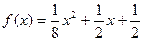 (3)
(3)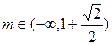
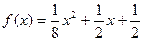 (3)
(3)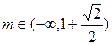
(1)由条件知 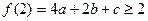 恒成立
恒成立
又∵取x=2时,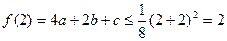 与恒成立,
与恒成立,
∴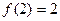 .
.
(2)∵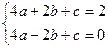 ∴
∴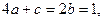 ∴
∴ .
.
又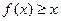 恒成立,即
恒成立,即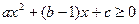 恒成立.
恒成立.
∴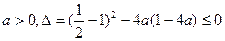 ,
,
解出: ,
,
∴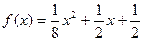 .
.
(3)由分析条件知道,只要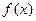 图象(在y轴右侧)总在直线
图象(在y轴右侧)总在直线 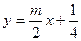 上方即可,也就是直线的斜率
上方即可,也就是直线的斜率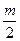 小于直线与抛物线相切时的斜率位置,于是:
小于直线与抛物线相切时的斜率位置,于是:
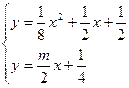
∴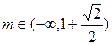 .
.
解法2: 必须恒成立,
必须恒成立,
即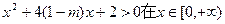 恒成立.
恒成立.
①△<0,即 [4(1-m)]2-8<0,解得: ;
;
②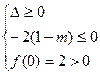 解出:
解出: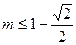 .
.
总之,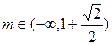 .
.
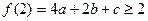 恒成立
恒成立又∵取x=2时,
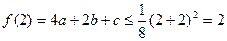 与恒成立,
与恒成立,∴
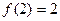 .
.(2)∵
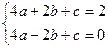 ∴
∴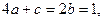 ∴
∴ .
. 又
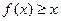 恒成立,即
恒成立,即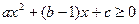 恒成立.
恒成立.∴
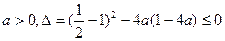 ,
,解出:
 ,
,∴
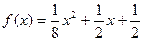 .
.(3)由分析条件知道,只要
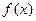 图象(在y轴右侧)总在直线
图象(在y轴右侧)总在直线 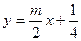 上方即可,也就是直线的斜率
上方即可,也就是直线的斜率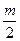 小于直线与抛物线相切时的斜率位置,于是:
小于直线与抛物线相切时的斜率位置,于是: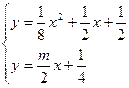
∴
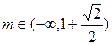 .
.解法2:
 必须恒成立,
必须恒成立,即
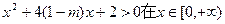 恒成立.
恒成立.①△<0,即 [4(1-m)]2-8<0,解得:
 ;
;②
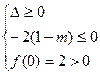 解出:
解出: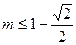 .
. 总之,
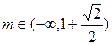 .
.
练习册系列答案
相关题目
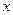 的不等式x2-(a+1)x+a<0
的不等式x2-(a+1)x+a<0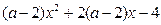 <0对一切实数x恒成立,求实数a的取值范围.
<0对一切实数x恒成立,求实数a的取值范围. 的不等式
的不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围. ,求
,求 的最小值。
的最小值。 ,则不等式
,则不等式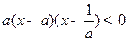 的解集是 (
的解集是 (  )
)