题目内容
10. 如图所示,正方体ABCD-A1B1C1D1的棱长为a,点P是棱AD上一点,且AP=$\frac{a}{3}$,过点B1,D1,P的平面交底面ABCD于PQ,Q在直线CD上,则PQ=$\frac{\sqrt{2}a}{3}$.
如图所示,正方体ABCD-A1B1C1D1的棱长为a,点P是棱AD上一点,且AP=$\frac{a}{3}$,过点B1,D1,P的平面交底面ABCD于PQ,Q在直线CD上,则PQ=$\frac{\sqrt{2}a}{3}$.
分析 作出PQ,然后求解距离即可.
解答  解:连结BD,过P作PQ∥BD交AB于Q,
解:连结BD,过P作PQ∥BD交AB于Q,
因为正方体ABCD-A1B1C1D1的棱长为a,点P是棱AD上一点,且AP=$\frac{a}{3}$,
所以AQ=$\frac{a}{3}$,
则PQ=$\frac{\sqrt{2}a}{3}$.
故答案为:$\frac{\sqrt{2}a}{3}$.
点评 本题考查直线与平面平行的判定定理以及性质定理的应用,考查计算能力以及逻辑推理能力.

练习册系列答案
相关题目
5.在三棱锥A-BCD中,AC=BD=3,AD=BC=4,AB=CD=m,则m的取值范围是( )
| A. | (1,5) | B. | (1,7) | C. | ($\sqrt{7}$,7) | D. | ($\sqrt{7}$,5) |
2.如果y是x的函数,x=$\sqrt{t+1}$,y=$\sqrt{t-1}$,其中t>1,则y与x的函数表达式为( )
| A. | y=$\sqrt{{x}^{2}-2}$ (x>2) | B. | y=$\sqrt{x-2}$(x>2) | C. | y=$\sqrt{{x}^{2}-2}$ (x>$\sqrt{2}$) | D. | y=$\sqrt{x-2}$(x>$\sqrt{2}$) |
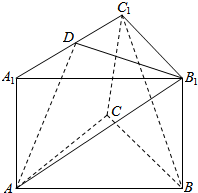 如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长为$\frac{\sqrt{2}}{2}$a,点D在棱A1C1上.
如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长为$\frac{\sqrt{2}}{2}$a,点D在棱A1C1上.