题目内容
已知直线l垂直平面a,垂足为O.在矩形ABCD中AD=1,AB=2,若点A在l上移动,点 B在平面a上移动,则O、D两点间的最大距离为
A. | B. | C. | D. |
B
试题分析:因为当点点A在l上移动,点 B在平面a上移动,那么可知点B到直线L的距离为x,那么AO=
 ,同时有AD=1,那么结合余弦定理则有
,同时有AD=1,那么结合余弦定理则有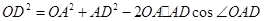 ,那么将数值代入表达式可知
,那么将数值代入表达式可知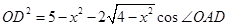 ,结合根式和二次函数的性质可知O、D两点间的最大距离为
,结合根式和二次函数的性质可知O、D两点间的最大距离为 ,选B.
,选B.点评:解决该试题的关键是利用线段AB的定长为2,AD为1,那么随着点A.B的运动过程中,始终保持不变的量和改变的角度OAD之间的关系式来求解OD的最大值,采用余弦定理得到分析证明,属于难度试题。

练习册系列答案
相关题目
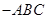 中
中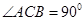 ,
,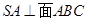 ,
,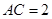 ,
,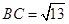 ,
,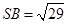 .
.
 。
。 与底面
与底面 所成二面角的大小。
所成二面角的大小。 中,底面
中,底面 是直角梯形,AB∥CD,∠ABC=
是直角梯形,AB∥CD,∠ABC= ,AB=PB=PC=BC=2CD=2,平面PBC⊥平面ABCD
,AB=PB=PC=BC=2CD=2,平面PBC⊥平面ABCD
 的值。若不存在,请说明理由。
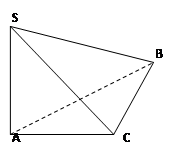
的值。若不存在,请说明理由。 是边长为4的正三角形,平面SAC⊥平面ABC,SA =" SC" =
是边长为4的正三角形,平面SAC⊥平面ABC,SA =" SC" =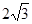 ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。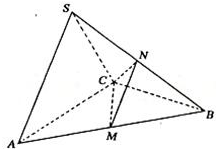
 所在平面与正
所在平面与正 所在平面互相垂直,
所在平面互相垂直, 分别为
分别为 的中点.
的中点.
 -
- 的体积;
的体积; 平面
平面 ;
; 上是否存在一点
上是否存在一点 ,使得平面
,使得平面 平面
平面 ?若存在,试指出点
?若存在,试指出点 的底面
的底面 为菱形,
为菱形,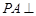 平面
平面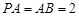 , E、F分别为
, E、F分别为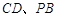 的中点,
的中点,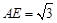 .
.
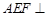 平面
平面 .
. 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.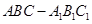 中,底面是正三角形,侧棱
中,底面是正三角形,侧棱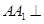 底面
底面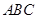 ,点
,点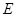 是侧面
是侧面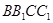 的中心,若
的中心,若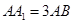 ,则直线
,则直线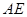 与平面
与平面
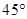


 的长轴为
的长轴为
 ,短轴为
,短轴为
 ,将椭圆沿y轴折成一个二面角,使得
,将椭圆沿y轴折成一个二面角,使得 中,
中,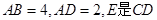 的中点,F为BC的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且
的中点,F为BC的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且 .
.
