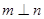题目内容
(14分)如图,在三棱锥S—ABC中,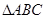 是边长为4的正三角形,平面SAC⊥平面ABC,SA =" SC" =
是边长为4的正三角形,平面SAC⊥平面ABC,SA =" SC" =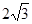 ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。
⑴ 求证:AC⊥SB;
⑵ 求二面角N—CM—B的正切值;
⑶ 求点B到平面CMN的距离。
 是边长为4的正三角形,平面SAC⊥平面ABC,SA =" SC" =
是边长为4的正三角形,平面SAC⊥平面ABC,SA =" SC" =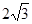 ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。
⑴ 求证:AC⊥SB;
⑵ 求二面角N—CM—B的正切值;
⑶ 求点B到平面CMN的距离。
⑴取AC中点O,连结OS、OB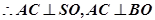 ∴SO⊥平面ABC,SO⊥BO如图建立空间直角坐标系O—xyz
∴SO⊥平面ABC,SO⊥BO如图建立空间直角坐标系O—xyz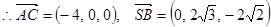
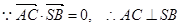 ⑵
⑵ 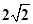 ⑶
⑶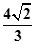
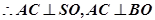 ∴SO⊥平面ABC,SO⊥BO如图建立空间直角坐标系O—xyz
∴SO⊥平面ABC,SO⊥BO如图建立空间直角坐标系O—xyz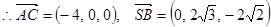
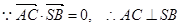 ⑵
⑵ 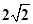 ⑶
⑶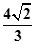
试题分析:⑴ 取AC中点O,连结OS、OB
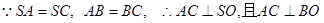
∵平面
 平面ABC,平面SAC
平面ABC,平面SAC 平面ABC=AC
平面ABC=AC∴SO⊥平面ABC, SO⊥BO
如图建立空间直角坐标系O—xyz
则
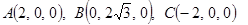
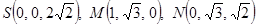
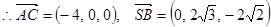
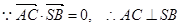
⑵ 由⑴得
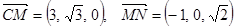
设
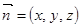 为平面CMN的一个法向量,则
为平面CMN的一个法向量,则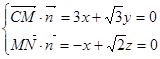 ,取
,取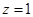
则
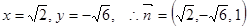
又
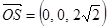 为平面ABC的一个法向量
为平面ABC的一个法向量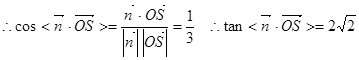
⑶ 由⑴⑵得
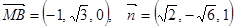 为平面CMN的一个法向量
为平面CMN的一个法向量∴点B到平面CMN的距离
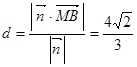 ……14分
……14分点评:本题的关键是由已知条件找到建立空间直角坐标系的合适位置,进而找到相关点,向量的坐标,代入线面角点面距的向量计算公式求解,有一定的难度

练习册系列答案
相关题目
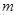 、
、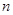 是不同的直线,
是不同的直线,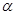 、
、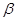 、
、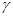 是不同的平面,有以下四命题:
是不同的平面,有以下四命题: 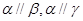 ,则
,则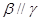 ; ②若
; ②若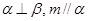 ,则
,则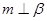 ;
;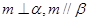 ,则
,则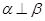 ; ④若
; ④若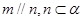 ,则
,则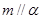 .
.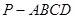 中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形, ,且
,且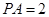 ,
,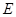 为
为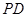 中点.
中点.
 平面
平面 的余弦值.
的余弦值.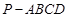 中,底面
中,底面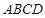 是正方形.已知
是正方形.已知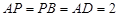 ,
,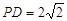 .
.
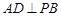 ;
;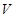 .
. 是
是 的中点,P点在侧面△SCD内及其边界上运动,并且总是保持
的中点,P点在侧面△SCD内及其边界上运动,并且总是保持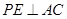 .则动点
.则动点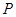 的轨迹与△
的轨迹与△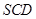 组成的相关图形最有可有是图中的( )
组成的相关图形最有可有是图中的( )
 α,n
α,n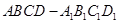 中,E,F满足
中,E,F满足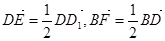 .
.
 ;
;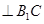 ;
;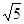
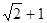
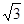
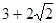
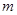 、
、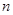 是两条不同的直线,
是两条不同的直线,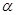 、
、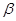 是两个不同的平面,则下列命题中不正确的是( )
是两个不同的平面,则下列命题中不正确的是( )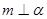 ,则
,则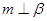

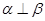
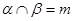 ,
,