题目内容
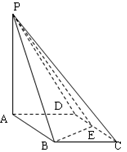
(本题满分16分)如图:AD=2,AB=4的长方形 所在平面与正
所在平面与正 所在平面互相垂直,
所在平面互相垂直, 分别为
分别为 的中点.
的中点.

(1)求四棱锥 -
- 的体积;
的体积;
(2)求证: 平面
平面 ;
;
(3)试问:在线段 上是否存在一点
上是否存在一点 ,使得平面
,使得平面 平面
平面 ?若存在,试指出点
?若存在,试指出点 的位置,并证明你的结论;若不存在,请说明理由.
的位置,并证明你的结论;若不存在,请说明理由.
 所在平面与正
所在平面与正 所在平面互相垂直,
所在平面互相垂直, 分别为
分别为 的中点.
的中点.
(1)求四棱锥
 -
- 的体积;
的体积;(2)求证:
 平面
平面 ;
;(3)试问:在线段
 上是否存在一点
上是否存在一点 ,使得平面
,使得平面 平面
平面 ?若存在,试指出点
?若存在,试指出点 的位置,并证明你的结论;若不存在,请说明理由.
的位置,并证明你的结论;若不存在,请说明理由.(1) ;(2)连
;(2)连 交
交 于
于 ,连
,连 则
则 为
为 中点,因为
中点,因为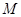 为
为 中点,所以
中点,所以 ,又
,又 ,
,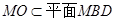 ,则
,则 .
.
(3)当BN=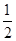 时,平面
时,平面 .
.
 ;(2)连
;(2)连 交
交 于
于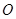 ,连
,连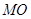 则
则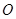 为
为 中点,因为
中点,因为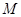 为
为 中点,所以
中点,所以 ,又
,又 ,
,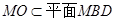 ,则
,则 .
. (3)当BN=
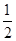 时,平面
时,平面 .
. 试题分析:(1)解:正
 中,Q为
中,Q为 的中点故
的中点故
由
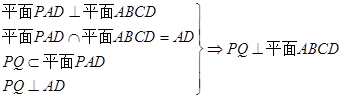 .
. 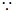

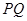 长为
长为 到平面
到平面 的距离.因为
的距离.因为 ,所以
,所以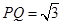
所以,

(2)证明:连
 交
交 于
于 ,连
,连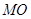 则
则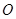 为
为 中点,因为
中点,因为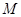 为
为 中点,
中点,所以
 , 又
, 又 ,
,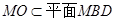 ,则
,则 .
. (3)当BN=
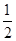 时,平面
时,平面 .
. 证明如下:由(1)证明知
 ,又
,又 ,则
,则
又因为长方形
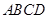 中由相似三角形得,则
中由相似三角形得,则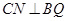
 又
又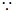
 所以,平面
所以,平面 .
. 点评:空间问题中的线面关系的证明主要是应用线面平行与垂直的判定定理或性质,具体问题中要是能够根据题意适当做辅助线;求简单几何体的体积问题关键是能够应用转化思想,将所求几何体的体积转化为易于求解底面积和高的几何体的体积,注意对等积法的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的底面为菱形,且
的底面为菱形,且 ,
,
 ,
, 为
为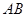 的中点.
的中点.

 平面
平面 ;
; 到面
到面 的距离.
的距离. 中,底面
中,底面 是正方形.已知
是正方形.已知 ,
, .
.
 ;
; .
. α,n
α,n 中,E,F满足
中,E,F满足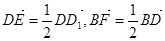 .
.
 ;
; ;
;
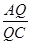 的值;若不存在,说明理由。
的值;若不存在,说明理由。



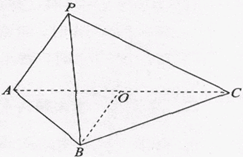
 BCD=60
BCD=60 ,E是CD的中点,PA
,E是CD的中点,PA 底面ABCD,PA=2.
底面ABCD,PA=2.