题目内容
已知向量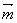 =(
=(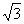 sin2x+2,cosx),
sin2x+2,cosx),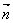 =(1,2cosx),设函数f(x)=
=(1,2cosx),设函数f(x)= 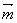 ·
·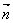 .
.
(I)求f(x)的最小正周期与单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,若a=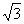 ,f(A)=4,求b+c的最大值.
,f(A)=4,求b+c的最大值.
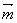 =(
=(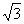 sin2x+2,cosx),
sin2x+2,cosx),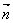 =(1,2cosx),设函数f(x)=
=(1,2cosx),设函数f(x)= 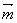 ·
·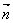 .
.(I)求f(x)的最小正周期与单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,若a=
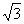 ,f(A)=4,求b+c的最大值.
,f(A)=4,求b+c的最大值.(1)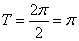
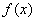 的单调递增区间为
的单调递增区间为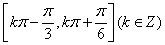
(2)当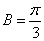 时,
时,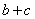 最大为
最大为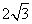
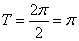
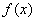 的单调递增区间为
的单调递增区间为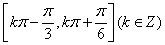
(2)当
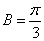 时,
时,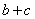 最大为
最大为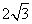
试题分析:解:(Ⅰ)
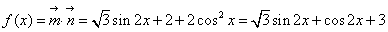
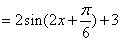 3分
3分∴
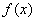 的最小正周期
的最小正周期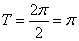 4分
4分由
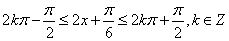 得
得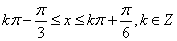
∴
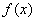 的单调递增区间为
的单调递增区间为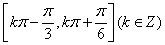 6分
6分(Ⅱ)由
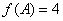 得
得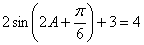 ,
,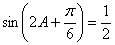
∵
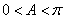 ∴
∴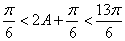 ∴
∴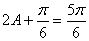 ,
,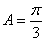 8分
8分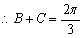
法一:又
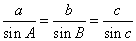 ,
,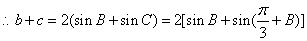
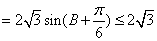
∴当
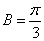 时,
时,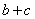 最大为
最大为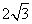 12分
12分法二:
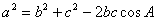
即
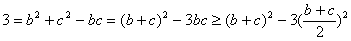
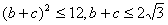 ;当且仅当
;当且仅当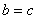 时等号成立。 12分
时等号成立。 12分点评:解决的关键是结合向量的数量积表示三角关系式,然后借助于三角函数的性质来得到求解,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
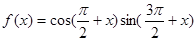 ,给出下列四个结论:①函数
,给出下列四个结论:①函数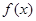 的最小正周期为
的最小正周期为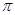 ;②若
;②若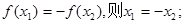 ③
③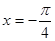 对称;④
对称;④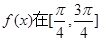 上是减函数,其中正确结论的个数为 ( )
上是减函数,其中正确结论的个数为 ( )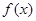 是定义域为
是定义域为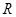 ,最小正周期为
,最小正周期为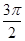 的函数。若
的函数。若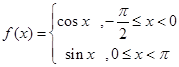 , 则
, 则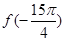 等于( )
等于( )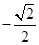
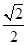
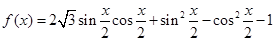 .
.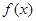 的最小正周期和值域;
的最小正周期和值域;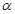 为第二象限角,且
为第二象限角,且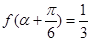 ,求
,求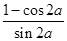 的值.
的值.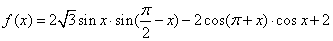 .
.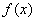 的最小正周期;
的最小正周期;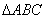 中,
中,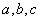 分别是
分别是 A、
A、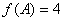 ,
,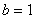 ,
,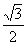 ,求
,求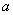 的值.
的值.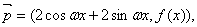
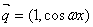 ,
,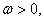
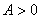 且
且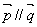 ,
,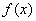 图象上相邻两条对称轴之间的距离是
图象上相邻两条对称轴之间的距离是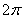 ,
,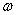 值;
值;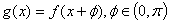 ,若
,若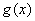 为偶函数,,求
为偶函数,,求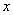 值
值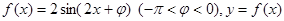 图像的一条对称轴是直线
图像的一条对称轴是直线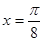 .
.
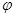 ;
;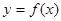 在区间
在区间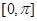 上的图像.
上的图像.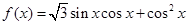 .
.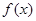 的最小正周期和单调增区间;
的最小正周期和单调增区间;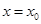 对称,且
对称,且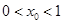 ,求
,求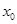 的值.
的值.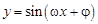
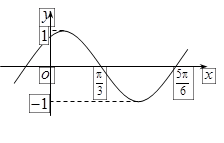
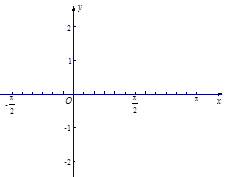
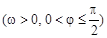 的部分图象如图所示,则点P
的部分图象如图所示,则点P 的坐标为( )
的坐标为( )