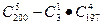题目内容
有A、B、C、D、E、F六人依次站在正六边形的六个顶点上传球,从A开始,每次可随意传给相邻的两人之一,若在5次之内传到D,则停止传球;若5次之内传不到D,则传完5次也停止传球,那么从开始到停止,可能出现的不同传法种数是( )
A.24 B.26 C.30 D.32
A.24 B.26 C.30 D.32
B
如右图所示,从A开始有两种传球方法:传给F或传给B,故有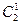 种传球方法;若传给F,则按如下树形图进行:
种传球方法;若传给F,则按如下树形图进行:
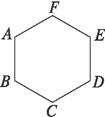
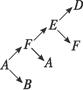
①若A→F→E→D,则传球终止,故有1种方法.
②若A→F→E→F,则需再传2次,有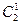
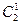 =4种方法.
=4种方法.
③若A→F→A,则需再传3次有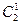
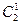
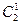 =8种方法.
=8种方法.
∴共有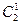 (1+4+8)=26种传球方法.
(1+4+8)=26种传球方法.
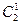 种传球方法;若传给F,则按如下树形图进行:
种传球方法;若传给F,则按如下树形图进行:

①若A→F→E→D,则传球终止,故有1种方法.
②若A→F→E→F,则需再传2次,有
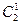
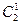 =4种方法.
=4种方法.③若A→F→A,则需再传3次有
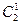
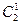
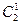 =8种方法.
=8种方法.∴共有
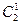 (1+4+8)=26种传球方法.
(1+4+8)=26种传球方法.
练习册系列答案
相关题目
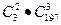 B.
B.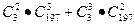
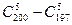 D.
D.