题目内容
从正方体的八个顶点中任取三个点为顶点作三角形，其中直角三角形的个数为( )
| A．56 | B．52 | C．48 | D．40 |
C.
从正方体的8个顶点中任取3个顶点可构成
个三角形，其中非直角三角形的有两类.
①上底面的每个顶点所在的两侧面对角线与下底面相应的对角线构成1个正三角形，上底面的4个顶点共构成4个非直角三角形；
②下底面的4个顶点所在的两侧面对角线与上底面相应的对角线共构成4个非直角三角形.
故所求直角三角形共有-4-4=48个.
个三角形，其中非直角三角形的有两类.①上底面的每个顶点所在的两侧面对角线与下底面相应的对角线构成1个正三角形，上底面的4个顶点共构成4个非直角三角形；
②下底面的4个顶点所在的两侧面对角线与上底面相应的对角线共构成4个非直角三角形.
故所求直角三角形共有
-4-4=48个.
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
个
},B={x|
},C={x|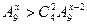
},全集U=A∪B∪C,现从U中每次取出2奇2偶四个数.
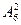+2
?
的各位数字之和等于7，那么称
若
则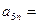
.