题目内容
在等差数列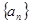 中,
中,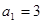 ,公差为
,公差为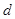 ,其前
,其前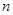 项和为
项和为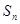 ,在等比数列
,在等比数列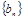 中,
中,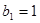 ,公比为
,公比为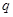 ,且
,且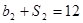 ,
,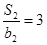 .
.
(1)求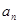 与
与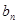 ;
;
(2)设数列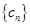 满足
满足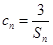 ,求
,求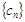 的前
的前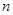 项和
项和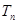 .
.
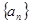 中,
中,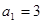 ,公差为
,公差为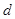 ,其前
,其前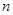 项和为
项和为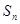 ,在等比数列
,在等比数列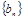 中,
中,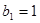 ,公比为
,公比为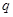 ,且
,且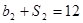 ,
,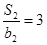 .
.(1)求
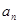 与
与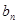 ;
;(2)设数列
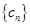 满足
满足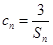 ,求
,求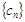 的前
的前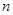 项和
项和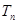 .
.(1)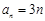 ,
,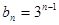 (2)
(2)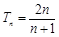 .
.
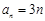 ,
,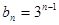 (2)
(2)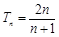 .
.试题分析:(1)求特殊数列(等差数列或等比数列)通项的基本方法就是待定系数法.本题中只需确定公差与公比,即只需列出两个独立条件就可解出.
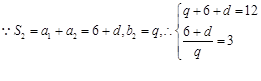 解得
解得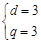 ,因此
,因此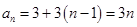 ,
,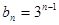 . (2)求数列前
. (2)求数列前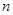 项和,首先先分析数列通项公式特点. 由(1)可知,
项和,首先先分析数列通项公式特点. 由(1)可知,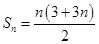 ,所以
,所以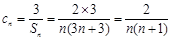 ,即是一个分式,可利用裂项相消法求和. 由
,即是一个分式,可利用裂项相消法求和. 由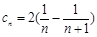 ,故
,故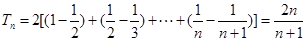
试题解析:解:(1)
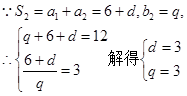 4分
4分故
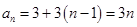 ,
,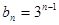 . 7分
. 7分(2)由(1)可知,
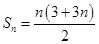 , 10分
, 10分所以
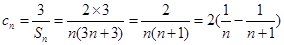 12分
12分故
 14分
14分
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 中,
中, ,且
,且 成等比数列.
成等比数列. ,试比较
,试比较 与
与 的大小,并说明理由.
的大小,并说明理由.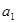 ,
, ,-1四个实数成等差数列,-4,
,-1四个实数成等差数列,-4,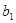 ,
,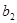 ,
,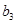 ,-1五个实数成等
,-1五个实数成等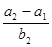 = .
= .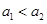 ,
,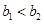 ,且
,且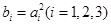 ,则
,则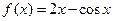 ,
,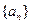 是公差为
是公差为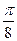 的等差数列,
的等差数列, ,则
,则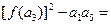 ( )
( )


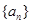 ,
,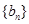 的前
的前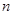 项和分别为
项和分别为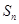 ,
,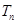 ,若
,若 ,则
,则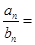 ( )
( )



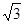 ,
,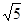 ,
,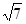 ,3,
,3,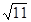 ,…,
,…,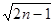 ,…,
,…,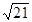 是这个数列的( )
是这个数列的( )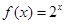 ,等差数列
,等差数列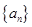 的公差为
的公差为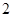 ,a1=1,则
,a1=1,则