题目内容
已知实数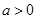 ,且
,且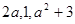 按某种顺序排列成等差数列.
按某种顺序排列成等差数列.
(1)求实数 的值;
的值;
(2)若等差数列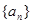 的首项和公差都为
的首项和公差都为 ,等比数列
,等比数列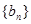 的首项和公比都为
的首项和公比都为 ,数列
,数列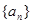 和
和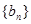 的前
的前 项和分别为
项和分别为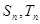 ,且
,且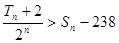 ,求满足条件的自然数
,求满足条件的自然数 的最大值.
的最大值.
(1)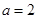 ;(2)14
;(2)14
解析试题分析:(1)由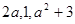 按某种顺序排列成等差数列,通过分类判断值的大小得到两类,再根据等差数列中项的性质,即可得到结论.
按某种顺序排列成等差数列,通过分类判断值的大小得到两类,再根据等差数列中项的性质,即可得到结论.
(2)由于等差数列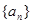 的首项和公差都为
的首项和公差都为 ,等比数列
,等比数列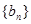 的首项和公比都为
的首项和公比都为 ,所以分别求出数列
,所以分别求出数列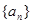 ,
,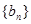 的通项公式.根据通项公式分别求出两个数列的前n项和的公式.再由
的通项公式.根据通项公式分别求出两个数列的前n项和的公式.再由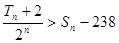 求出结论.
求出结论.
(3)解法一:由已知三个数有: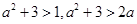 , 1分
, 1分
不妨设排列成递增的等差数列,则
①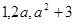 依次成等差数列,则有
依次成等差数列,则有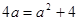 解得
解得 ,符合题意; 3分
,符合题意; 3分
②若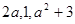 依次成等差数列,则有
依次成等差数列,则有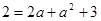 解得
解得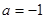 ,由
,由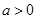 不符合题意; 5分
不符合题意; 5分
综上得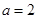 . 6分
. 6分
解法二:分三种情况讨论:
①若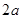 为等差中项,则有
为等差中项,则有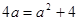 解得
解得 ,符合题意; 2分
,符合题意; 2分
②若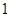 为等差中项,则有
为等差中项,则有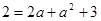 解得
解得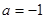 ,由
,由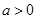 不符合题意; 4分
不符合题意; 4分
③若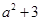 为等差中项,则有
为等差中项,则有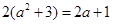 ,即
,即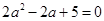 ,
, 方程无解; 6分
方程无解; 6分
综上得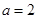 .
.
(2)解:由(1)知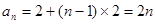 ,
,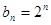 , 8分
, 8分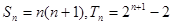 , 10分
, 10分
由已知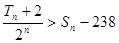 可得
可得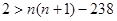 ,即
,即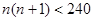 , 11分
, 11分
即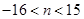 ,又
,又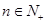 ,故
,故 的最大值为14. 12分
的最大值为14. 12分
考点:1.等差等比数列的通项公式.2.求和公式.3.不等式的交汇.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
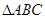 中,角
中,角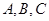 的对边分别为
的对边分别为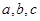 ,且
,且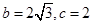 ,求
,求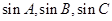 成等比数列,试判断
成等比数列,试判断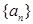 满足
满足 .
.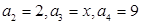 ,求
,求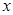 的取值范围;
的取值范围;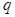 等比数列,
等比数列,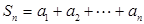 ,
,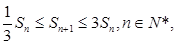 求
求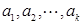 成等差数列,且
成等差数列,且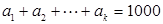 ,求正整数
,求正整数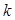 的最大值,以及
的最大值,以及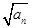 ,an+1)( n ∈N*)在函数y=x2+1的图象上.
,an+1)( n ∈N*)在函数y=x2+1的图象上.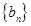 满足b1=1,
满足b1=1,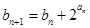 ,求证:
,求证: .
.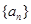 是等差数列,
是等差数列,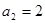 ,前四项和
,前四项和 。
。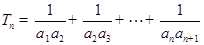 ,计算
,计算 。
。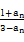 (n∈N*),且a1=
(n∈N*),且a1= .
.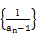 是等差数列,并求an.
是等差数列,并求an.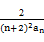 (n∈N*),求数列{bn}的前n项和Tn.
(n∈N*),求数列{bn}的前n项和Tn. 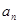 }中,
}中,  (1)求
(1)求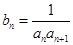 ,求
,求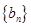 的前n项和
的前n项和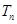 。
。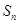 为等差数列
为等差数列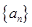 的前
的前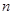 项和,已知
项和,已知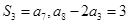 .
.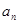 ;
;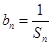 ,数列
,数列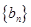 的前
的前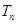 ,求证:
,求证: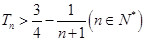 .
. 的公差大于零的等差数列,已知
的公差大于零的等差数列,已知 ,
, .
. 是以函数
是以函数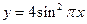 的最小正周期为首项,以
的最小正周期为首项,以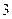 为公比的等比数列,求数列
为公比的等比数列,求数列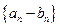 的前
的前 项和
项和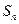 .
.