题目内容
17.各项均为正数的数列{bn}的前n项和为Sn,且对任意正整数n,都有2Sn=bn(bn+1).(1)求数列{bn}的通项公式;
(2)如果等比数列{an}共有m(m≥2,m∈N*)项,其首项与公比均为2,在数列{an}的每相邻两项ai与ai+1之间插入i个(-1)ibi(i∈N*)后,得到一个新的数列{cn}.求数列{cn}中所有项的和;
(3)如果存在n∈N*,使不等式 bn+$\frac{1}{b_n}≤(n+1)λ≤{b_{n+1}}+\frac{1}{{{b_{n+1}}}}$成立,求实数λ的范围.
分析 (1)当n=1时可得b1=1,当n≥2时,通过递推关系可得bn-bn-1=1,从而数列{bn}是首相与公差均为1等差数列,计算即可;
(2)通过${a_n}={2^n}$,分m=2k-1(k≥2,k∈N*)与m=2k(k∈N*)两种情况讨论即可;
(3)利用不等式的性质,化简可得$\frac{{n+\frac{1}{n}}}{n+1}≤λ≤1+\frac{1}{{{{(n+1)}^2}}},n=1,2,3,…$,记${A_n}=\frac{{n+\frac{1}{n}}}{n+1},{B_n}=1+\frac{1}{{{{(n+1)}^2}}},n=1,2,3,…$,只需求An的最大值、Bn的最小值即可.
解答 解:(1)当n=1时,由2S1=b1(b1+1)得b1=1,
当n≥2时,由2Sn=bn(bn+1)及2Sn-1=bn-1(bn-1+1),
可得2bn=2Sn-2Sn-1=bn(bn+1)-bn-1(bn-1+1),
即(bn+bn-1)(bn-bn-1)=bn+bn-1,
∵数列{bn}的各项均为正数,∴bn-bn-1=1,
∴数列{bn}是首相与公差均为1等差数列,
∴数列{bn}的通项公式为bn=n;
(2)通过题意,易得数列{an}的通项公式为${a_n}={2^n}$,
当m=2k-1(k≥2,k∈N*)时,
数列{cn}共有(2k-1)+1+2+…+(2k-2)=k(2k-1)项,
其所有项的和为${S_{k(2k-1)}}=(2+{2^2}+…+{2^{2k-1}})+[-1+{2^2}-{3^2}+{4^2}-…-{(2k-3)^2}+{(2k-2)^2}]$
=2(22k-1-1)+[3+7+…+(4k-5)]
=22k-2+(2k-1)(k-1)
=$\frac{1}{2}m(m-1)+{2^{m+1}}-2$;
当m=2k(k∈N*)时,数列{cn}共有2k+1+2+…+(2k-1)=k(2k+1)项,
其所有项的和为${S_{k(2k+1)}}={S_{k(2k-1)}}+{2^{2k}}-{(2k-1)^2}$
=22k-2+(2k-1)(k-1)+22k-(2k-1)2
=22k+1-k(2k-1)-2=$-\frac{1}{2}m(m-1)+{2^{m+1}}-2$;
(3)∵${b_n}+\frac{1}{b_n}≤(n+1)λ≤{b_{n+1}}+\frac{1}{{{b_{n+1}}}}$,
∴$\frac{{n+\frac{1}{n}}}{n+1}≤λ≤1+\frac{1}{{{{(n+1)}^2}}},n=1,2,3,…$
记${A_n}=\frac{{n+\frac{1}{n}}}{n+1},{B_n}=1+\frac{1}{{{{(n+1)}^2}}},n=1,2,3,…$
由${A_n}-{A_{n+1}}=\frac{2-n}{n(n+1)(n+2)}$,${B_n}-{B_{n+1}}=\frac{2n+3}{{{{(n+1)}^2}{{(n+2)}^2}}}$,
得A1>A2=A3,A3<A4<A5<…,B1>B2>B3>…
∴实数λ的范围为[A2,B1],即$[{\frac{5}{6},\frac{5}{4}}]$.
点评 本题考查数列的通项公式,前n项和公式,考查递推关系,考查分类讨论法,考查不等式的性质,注意解题方法的积累,属于难题.

| A. | .$±\frac{{\sqrt{7}}}{2}$ | B. | .$\frac{{\sqrt{7}}}{2}$ | C. | .$-\frac{{\sqrt{7}}}{2}$ | D. | $\frac{{\sqrt{7}}}{4}$ |
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | $\sqrt{19}$ | D. | $\sqrt{23}$ |
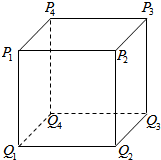 如图,正方体P1P2P3P4-Q1Q2Q3Q4的棱长为1,设
如图,正方体P1P2P3P4-Q1Q2Q3Q4的棱长为1,设 如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF⊥PB.
如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF⊥PB.