Question

2．如图，正方体P₁P₂P₃P₄-Q₁Q₂Q₃Q₄的棱长为1，设
x=$\overrightarrow{{P_1}{Q_1}}\overrightarrow{•{S_i}{T_j}}，（{{S_i}，{T_j}∈\left\{{{P_i}，{Q_j}}\right\}}），（{i，j∈\left\{{1，2，3，4}\right\}}）$，
对于下列命题：
①当$\overrightarrow{{S_i}{T_j}}=\overrightarrow{{P_i}{Q_i}}$时，x=1；
②当x=0时，（i，j）有12种不同取值；
③当x=-1时，（i，j）有16种不同的取值；
④x的值仅为-1，0，1．
其中正确的命题是（　　）

• A． ①②
• B． ①④
• C． ①③④
• D． ①②③④

Answer 1

分析 根据题意，建立空间直角坐标系，得出向量$\overrightarrow{{{P}_{i}Q}_{j}}$、$\overrightarrow{{{P}_{1}Q}_{1}}$、$\overrightarrow{{{P}_{i}P}_{j}}$、$\overrightarrow{{{Q}_{i}P}_{j}}$的坐标表示，求出x=$\overrightarrow{{{P}_{1}Q}_{1}}$$\overrightarrow{{{S}_{i}T}_{j}}$•的值即可判断所给的结论是否正确．

解答 解：根据题意，建立空间直角坐标系，如图所示；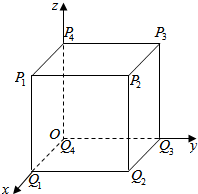

①当$\overrightarrow{{S_i}{T_j}}=\overrightarrow{{P_i}{Q_i}}$时，x=$\overrightarrow{{{P}_{1}Q}_{1}}$•$\overrightarrow{{{P}_{i}Q}_{j}}$=（-1，0，0）•（-1，x_i，x_j）=1，∴①正确；
②当 x=0时，i=1、2、3、4，j=1、2、3、4，（i，j）有4×4=16种不同的取值，∴②错误；
③当x=-1时，i=1、2、3、4，j=1、2、3、4，（i，j）有4×4=16种不同的取值，∴③正确；
④当 $\overrightarrow{{{S}_{i}T}_{j}}$=$\overrightarrow{{{P}_{i}Q}_{j}}$时，x=$\overrightarrow{{{P}_{1}Q}_{1}}$•$\overrightarrow{{{P}_{i}Q}_{j}}$=1，
当 $\overrightarrow{{{S}_{i}T}_{j}}$=$\overrightarrow{{{P}_{i}P}_{j}}$时，x=$\overrightarrow{{{P}_{1}Q}_{1}}$•$\overrightarrow{{{P}_{i}P}_{j}}$=（-1，0，0，）•（0，x_i，x_j）=0，
当 $\overrightarrow{{{S}_{i}T}_{j}}$=$\overrightarrow{{{Q}_{i}P}_{j}}$时，x=$\overrightarrow{{{P}_{1}Q}_{1}}$•$\overrightarrow{{{Q}_{i}P}_{j}}$=（-1，0，0）•（1，x_i，x_j）=-1，
∴x的取值仅为-1，0，1，∴④正确．
综上，正确的结论是①③④，
故选：C．

点评 本题考查了空间向量的应用问题，也考查了集合知识的应用问题，是综合性题目．