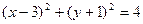题目内容
如如图:⊙ 与⊙
与⊙ 外切于
外切于 ,⊙
,⊙ ,⊙
,⊙ 的半径分别为
的半径分别为 .
. 为⊙
为⊙ 的切线,
的切线, 为⊙
为⊙ 的直径,
的直径, 分别交⊙
分别交⊙ ,⊙
,⊙ 于
于 ,则
,则 的值为:
的值为:

 与⊙
与⊙ 外切于
外切于 ,⊙
,⊙ ,⊙
,⊙ 的半径分别为
的半径分别为 .
. 为⊙
为⊙ 的切线,
的切线, 为⊙
为⊙ 的直径,
的直径, 分别交⊙
分别交⊙ ,⊙
,⊙ 于
于 ,则
,则 的值为:
的值为:
A.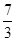 | B. | C.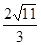 | D. |
D
分析:分别求出CD和PD的长度,再计算CD+3PD:
(1)由相似关系求PD的长度.连接O1O2,则O1O2过P点,三角形O1PD相似于O1BO2,由相似关系求出PD;
(2)由切割线定理求CD的长度.这个要分两步做:
①由勾股定理求出O1A、O1B的长度.在直角三角形O1O2A和O1AB中,分别用勾股定理求出O1A、O1B的长度;
②由切割线定理求O1D的长度.由切割线定理O1A2=O1D?O1B,所以O1D可求出来.而O1D=O1C+CD=2+CD,故CD可求.
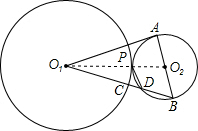
解:连接O1O2,
∵AO2=1,O1O2=3,
∴AO1=
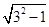 =2
=2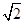 ,
,∴BO1=
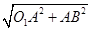 =
=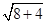 =2
=2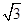 ,
,∴由切割线定理O1A2=O1D?O1B,得O1D=
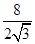 =
=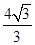 ,
,∴CD=O1D-O1C=
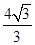 -2,
-2,又∵cos∠O2O1B=
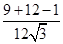 =
=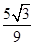 ,
,则PD2=4+
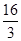 -
-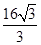 cos∠O2O1B=4+
cos∠O2O1B=4+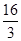 -
-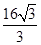 ×
×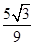 =
=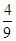 ,
,∴PD=
 ,
,∴CD+3PD=
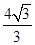 -2+3×
-2+3× =
=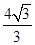 .
.故选D.

练习册系列答案
相关题目

 是半圆
是半圆 的直径,点
的直径,点 在半圆上,
在半圆上, 于点
于点 ,且
,且 ,设
,设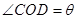 ,则
,则 =( )
=( )




 满足
满足
 的最大值。
的最大值。 的最小值。
的最小值。 外一点
外一点 引圆
引圆 和割线
和割线 ,已知
,已知 ,
, ,圆心
,圆心 的距离为
的距离为 ,则圆
,则圆
 关于直线
关于直线 :
: 对称的圆为
对称的圆为 .
. 和圆
和圆  求线段
求线段 长的最小值.(12分)
长的最小值.(12分)  是圆
是圆 的直径,
的直径,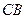 切圆
切圆 点,
点, 切圆
切圆 点,交
点,交 的延长线于E点,
的延长线于E点, 则
则 =____________;
=____________;
 ,设该圆过点
,设该圆过点 的最长弦和最短弦分别为
的最长弦和最短弦分别为 和
和 ,则四边形
,则四边形 的面积为
的面积为  ,且圆心在直线
,且圆心在直线 上的圆的方程是
上的圆的方程是