Question

【题目】已知在极坐标系中曲线C的极坐标方程为．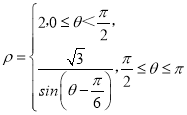

（1）求曲线C与极轴所在直线围成图形的面积；

（2）设曲线C与曲线ρsinθ＝1交于A，B，求|AB|．

Answer 1

【答案】（1）；（2）2．

【解析】

（1）直接利用转换关系，将曲线C的极坐标方程转化为直角坐标方程，得到曲线C与极轴所在直线围成的图形是一个半径为2的圆周及一个两直角边分别为2与2的直角三角形，即可求得面积.

（2）联立方程组，分别求出A和B的坐标，再利用两点间的距离公式求出结果．

（1）因为曲线C的极坐标方程为，

所以当 时，，

当 时，x，

所以曲线C与极轴所在直线围成的图形是一个半径为2的圆周及一个两直角边分别为2与2的直角三角形，

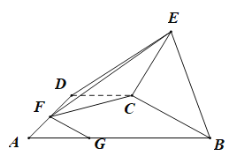
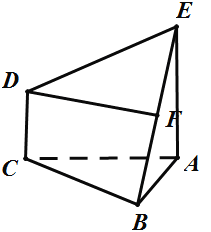
如图所示：

所以．

（2）因为曲线C与曲线ρsinθ＝1交于A，B，

由，得A（2，），转换为直角坐标为A（）．

极坐标方程ρsinθ＝1转换为直角坐标方程为y＝1，

极坐标方程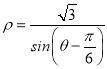转换为直角坐标方程为x，

所以B（），

所以|AB|＝．