题目内容
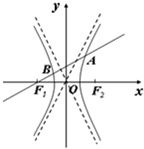
已知F为椭圆
+
=1（a＞b＞0）的右焦点，直线l过点F且与双曲线
-
=1的两条渐近线l1，l2分别交于点M，N，与椭圆交于点A，B．
（Ⅰ）若∠MON=
，双曲线的焦距为4．求椭圆方程．
（Ⅱ）若
•
=0（O为坐标原点），
=
，求椭圆的离心率e．
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
（Ⅰ）若∠MON=
| π |
| 3 |
（Ⅱ）若
| OM |
| MN |
| FA |
| 1 |
| 3 |
| AN |
（Ⅰ）∵双曲线
-
=1的焦点在x轴上，
∴渐近线方程为y=±
x
∴渐近线l1的斜率为
又∵∠MON=
，M，N是直线l与双曲线两条渐近线l1，l2的交点，
∴渐近线l1的倾斜角为
，
∴
=tan
=
，即a=
b
∵双曲线的焦距为4，
∴a2+b2=4．
把a=
b代入，得，a2=3，b2=1
∴椭圆方程为
+y2=1
（Ⅱ）设椭圆的焦距为2c，则点F的坐标为（c，0）
∵
•
=0，∴l⊥l1
∵直线l1的方程为y=-
x，∴直线l的斜率为
，
∴直线l的方程为y=
(x-c)
联立l1，l方程，由
解得
即点N(
，
)
设A（x，y），由
=
，得(x-c，y)=
(
-x，
-y)
即
，解得，
∴A(
，
)
∵点A在椭圆上，代入椭圆方程，得
+
=1
即（3c2+a2）2+a4=16a2c2，
∴（3e2+1）2+1=16e2，即9e4-10e2+2=0
解得e2=
∴e=
椭圆的离心率是e=
| x2 |
| a2 |
| y2 |
| b2 |
∴渐近线方程为y=±
| b |
| a |
∴渐近线l1的斜率为
| b |
| a |
又∵∠MON=
| π |
| 3 |
∴渐近线l1的倾斜角为
| π |
| 6 |
∴
| b |
| a |
| π |
| 6 |
| ||
| 3 |
| 3 |
∵双曲线的焦距为4，
∴a2+b2=4．
把a=
| 3 |
∴椭圆方程为
| x2 |
| 3 |
（Ⅱ）设椭圆的焦距为2c，则点F的坐标为（c，0）
∵
| OM |
| ON |
∵直线l1的方程为y=-
| b |
| a |
| a |
| b |
∴直线l的方程为y=
| a |
| b |
联立l1，l方程，由
|
|
即点N(
| a2 |
| c |
| ab |
| c |
设A（x，y），由
| FA |
| 1 |
| 3 |
| AN |
| 1 |
| 3 |
| a2 |
| c |
| ab |
| c |
即
|
|
∴A(
| 3c2+a2 |
| 4c |
| ab |
| 4c |
∵点A在椭圆上，代入椭圆方程，得
| (3c2+a2)2 |
| 16a2c2 |
| a2 |
| 16c2 |
即（3c2+a2）2+a4=16a2c2，
∴（3e2+1）2+1=16e2，即9e4-10e2+2=0
解得e2=
5±
| ||
| 9 |
∴e=
| ||||
| 3 |
椭圆的离心率是e=
| ||||
| 3 |
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
