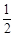题目内容
设经过双曲线x2-
=1的左焦点F1作倾斜角为
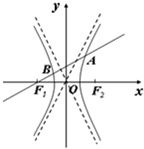
的直线与双曲线左右两支分别交于点A,B.求
(I)线段AB的长;
(II)设F2为右焦点,求△F2AB的周长.
| y2 |
| 3 |
| π |
| 6 |
(I)线段AB的长;
(II)设F2为右焦点,求△F2AB的周长.

(I)F1(-2,0)
k=tan
=
设A(x1,y1)B(x2,y2)
将直线AB:y=
(x+2)代入3x2-y2-3=0
整理得8x2-4x-13=0
由距离公式|AB|=
=3(6分)
(II)|F2A|=2x1-1,|F2B|=1-2x2
∴|F2A|+|F2B|=2(x1-x2)=2•
=2•
=3
∴△F2AB的周长L=3+3
(12分)
k=tan
| π |
| 6 |
| ||
| 3 |
设A(x1,y1)B(x2,y2)
将直线AB:y=
| ||
| 3 |
整理得8x2-4x-13=0
由距离公式|AB|=
| 1+k2 |
| ||
| 8 |
(II)|F2A|=2x1-1,|F2B|=1-2x2
∴|F2A|+|F2B|=2(x1-x2)=2•
| (x1+x2)2-4x1x2 |
| 3 |
| 2 |
| 3 |
| 3 |
∴△F2AB的周长L=3+3
| 3 |

练习册系列答案
相关题目
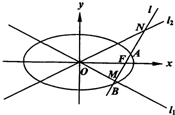
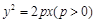 的准线与圆
的准线与圆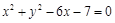 相切,则
相切,则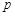 的值为
的值为