题目内容
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=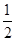 AB.直角梯形ACEF中,
AB.直角梯形ACEF中,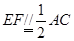 ,
,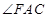 是锐角,且平面ACEF⊥平面ABCD.
是锐角,且平面ACEF⊥平面ABCD.
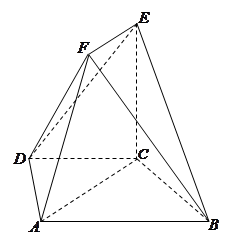
(1)求证: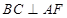 ;
;
(2)试判断直线DF与平面BCE的位置关系,并证明你的结论.
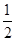 AB.直角梯形ACEF中,
AB.直角梯形ACEF中,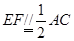 ,
,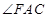 是锐角,且平面ACEF⊥平面ABCD.
是锐角,且平面ACEF⊥平面ABCD.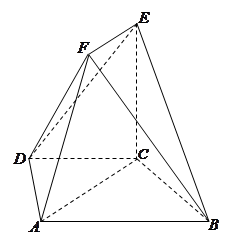
(1)求证:
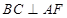 ;
;(2)试判断直线DF与平面BCE的位置关系,并证明你的结论.
(1)详见试题解析;(2)DF∥平面BCE.证明详见试题解析.
试题分析:(1)证明线线垂直,可转化为证明线面垂直.要证
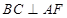 ,只要证
,只要证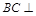 平面
平面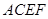 ,由已知平面ACEF⊥平面ABCD,故由面面垂直的性质定理知,只要证
,由已知平面ACEF⊥平面ABCD,故由面面垂直的性质定理知,只要证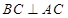 .在等腰梯形ABCD中,由已知条件及平面几何相关知识,易得
.在等腰梯形ABCD中,由已知条件及平面几何相关知识,易得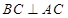 ;(2)首先给出结论DF∥平面BCE,再给出证明.要证线面平行,由利用判定定理可以转化为证明线线平行,即只要在平面BCE找DF的平行线,或由面面平行的性质定理转化为证明面面平行,即过DF找一个平面与平面BCE平行,而后一种方法容易实施.
;(2)首先给出结论DF∥平面BCE,再给出证明.要证线面平行,由利用判定定理可以转化为证明线线平行,即只要在平面BCE找DF的平行线,或由面面平行的性质定理转化为证明面面平行,即过DF找一个平面与平面BCE平行,而后一种方法容易实施.试题解析:(1)证明:取AB中点H,连结CH.
 底面ABCD是梯形,且AD=DC=CB=
底面ABCD是梯形,且AD=DC=CB=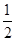 AB,易证四边形AHCD为平行四边形,
AB,易证四边形AHCD为平行四边形,∴AD=HC=
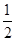 AB,
AB,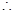
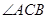 =
=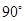
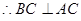 , 3分
, 3分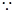 平面
平面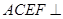 平面
平面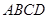 ,且平面
,且平面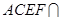 平面
平面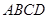
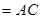 ,
,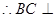 平面
平面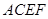 ,而
,而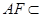 平面
平面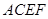 ,故
,故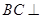
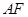 . 6分
. 6分(2)
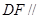 平面
平面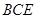 ,以下证明:
,以下证明:取AC的中点M,连接DM,FM.在平面ABCD中,DM,BC⊥AC,故DM∥BC. 8分

在直角梯形ACEF中,
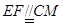 ,故FM∥EC. 10分
,故FM∥EC. 10分而BC,CE
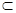 平面BCE,BC∩CE=C,而DM,MF
平面BCE,BC∩CE=C,而DM,MF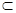 平面DMF,DM∩MF=M,故平面BCE∥平面DMF,DF
平面DMF,DM∩MF=M,故平面BCE∥平面DMF,DF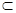 平面DMF,从而,DF∥平面BCE. 12分
平面DMF,从而,DF∥平面BCE. 12分
练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
给出下列命题:
①没有公共点的两条直线平行;
②互相垂直的两条直线是相交直线;
③既不平行也不相交的直线是异面直线;
④不同在任一平面内的两条直线是异面直线.
其中正确命题的个数是( )
①没有公共点的两条直线平行;
②互相垂直的两条直线是相交直线;
③既不平行也不相交的直线是异面直线;
④不同在任一平面内的两条直线是异面直线.
其中正确命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |

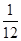 ·VABC-A1B1C1,求A1E的长度.
·VABC-A1B1C1,求A1E的长度.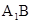 的中点,F是棱CC1上的点.
的中点,F是棱CC1上的点.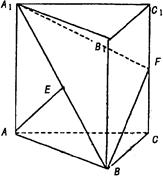
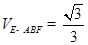 时,求正方形AA1C1C的边长;
时,求正方形AA1C1C的边长;