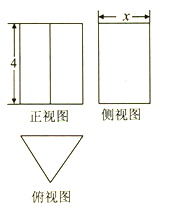
题目内容
【题目】在集合![]() 中,任取
中,任取![]() 个元素构成集合
个元素构成集合![]() . 若
. 若![]() 的所有元素之和为偶数,则称
的所有元素之和为偶数,则称![]() 为
为![]() 的偶子集,其个数记为
的偶子集,其个数记为![]() ;若
;若![]() 的所有元素之和为奇数,则称
的所有元素之和为奇数,则称![]() 为
为![]() 的奇子集,其个数记为
的奇子集,其个数记为![]() . 令
. 令![]()
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)求![]() .
.
【答案】(1)![]() ,
,![]() ,
,![]() ,(2)
,(2)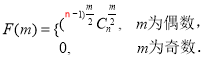
【解析】
试题(1)第一小问是具体理解及时定义:当![]() 时,集合为
时,集合为![]() ,当
,当![]() 时,偶子集有
时,偶子集有![]() ,奇子集有
,奇子集有![]() ,
,![]() ,
,![]() ;同理可得
;同理可得![]() ,
,![]() ,(2)从具体到一般,是归纳:当
,(2)从具体到一般,是归纳:当![]() 为奇数时,偶子集的个数等于奇子集的个数,
为奇数时,偶子集的个数等于奇子集的个数,![]() ;当
;当![]() 为偶数时,偶子集的个数
为偶数时,偶子集的个数![]() ,奇子集的个数
,奇子集的个数![]() ,
,
涉及两个组合数相乘:构造二项展开式![]() ,比较对应项
,比较对应项![]() 的系数
的系数
试题解析:解(1)当![]() 时,集合为
时,集合为![]() ,
,
当![]() 时,偶子集有
时,偶子集有![]() ,奇子集有
,奇子集有![]() ,
,![]() ,
,![]() ;
;
当![]() 时,偶子集有
时,偶子集有![]() ,奇子集有
,奇子集有![]() ,
,
![]() ,
,![]() ;
;
当![]() 时,偶子集有
时,偶子集有![]() ,奇子集有
,奇子集有![]() ,
,
![]() ,
,![]() ;
;
(2)当![]() 为奇数时,偶子集的个数
为奇数时,偶子集的个数![]() ,
,
奇子集的个数![]() ,
,
所以![]() .
.
当![]() 为偶数时,偶子集的个数
为偶数时,偶子集的个数![]() ,
,
奇子集的个数![]() ,
,
所以![]()
![]() .
.
一方面,
![]()
所以![]() 中
中![]() 的系数为
的系数为
![]() ;
;
另一方面,![]() ,
,![]() 中
中![]() 的系数为
的系数为![]() ,
,
故![]()
![]() .
.
综上,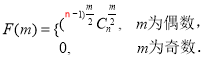

【题目】继共享单车之后,又一种新型的出行方式------“共享汽车”也开始亮相北上广深等十余大中城市,一款叫“一度用车”的共享汽车在广州提供的车型是“奇瑞eQ”,每次租车收费按行驶里程加用车时间,标准是“1元/公里+0.1元/分钟”,李先生家离上班地点10公里,每天租用共享汽车上下班,由于堵车因素,每次路上开车花费的时间是一个随机变量,根据一段时间统计40次路上开车花费时间在各时间段内的情况如下:
时间(分钟) |
|
|
|
|
|
次数 | 8 | 14 | 8 | 8 | 2 |
以各时间段发生的频率视为概率,假设每次路上开车花费的时间视为用车时间,范围为![]() 分钟.
分钟.
(Ⅰ)若李先生上.下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设![]() 是4次使用共享汽车中最优选择的次数,求
是4次使用共享汽车中最优选择的次数,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).