题目内容
命题A:(x-1)2<9,命题B:(x+2)·(x+a)<0;若A是B的充分不必要条件,则a的取值范围是( )
| A.(-∞,-4) | B.[4,+∞) | C.(4,+∞) | D.(-∞,-4] |
A
本题考查的知识点是充要条件与集合之间的关系,其中根据“谁小谁充分,谁大谁必要”的原则,将充要条件问题转化为集合关系问题是解答本题的关键.
由|x-1|<3,得-2<x<4,∴命题A:-2<x<4.命题B:当a=2时,x∈φ,当a<2时,-2<x<-a,当a>2时,-a<x<-2.∵A是B的充分而不必要条件,∴命题B:当a<2时,-2<x<-a,∴-a>4,∴a<-4,综上,当a<-4时,A是B的充分不必要条件,故选A.
解题的关键是解不等式我们可以求出命题A与命题B中x的取值范围,然后根据“谁小谁充分,谁大谁必要”的原则,结合A是B的充分不必要条件,则A?B,将问题转化为一个集合关系问题,分析参数a的取值后,即可得到结论.
由|x-1|<3,得-2<x<4,∴命题A:-2<x<4.命题B:当a=2时,x∈φ,当a<2时,-2<x<-a,当a>2时,-a<x<-2.∵A是B的充分而不必要条件,∴命题B:当a<2时,-2<x<-a,∴-a>4,∴a<-4,综上,当a<-4时,A是B的充分不必要条件,故选A.
解题的关键是解不等式我们可以求出命题A与命题B中x的取值范围,然后根据“谁小谁充分,谁大谁必要”的原则,结合A是B的充分不必要条件,则A?B,将问题转化为一个集合关系问题,分析参数a的取值后,即可得到结论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
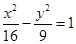 与椭圆
与椭圆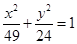 有相同的焦点;
有相同的焦点; 、
、 为两个定点,
为两个定点,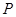 为动点,且
为动点,且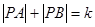 ,其中常数
,其中常数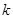 为正实数,则动点
为正实数,则动点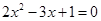 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;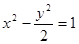 的右焦点
的右焦点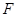 作直线
作直线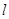 交双曲线于
交双曲线于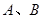 两点,若
两点,若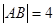 ,则这样的直线
,则这样的直线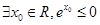
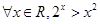
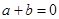 的充要条件是
的充要条件是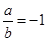
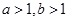 是
是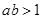 的充分条件
的充分条件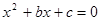 有一根大于1,另一根小于1的充要条件是
有一根大于1,另一根小于1的充要条件是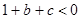
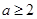 时,
时,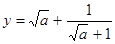 的最小值为1
的最小值为1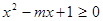 对于
对于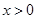 恒成立,则
恒成立,则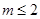
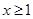 的一个充分不必要条件是
的一个充分不必要条件是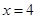
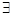 x∈R,使得x2+1>3x”的否定是“
x∈R,使得x2+1>3x”的否定是“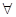 x∈R,都有x2+1≤3x”;
x∈R,都有x2+1≤3x”;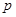 、q是简单命题,若“
、q是简单命题,若“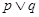 ”为假命题,则“
”为假命题,则“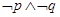 ” 为真命题;
” 为真命题;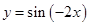
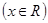 的图像上所有的点向右平移
的图像上所有的点向右平移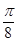 个单位即可得到函数
个单位即可得到函数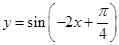
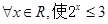 ”的否定是“
”的否定是“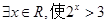 ”;
”;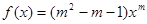 是幂函数,且在
是幂函数,且在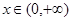 上为增函数,则
上为增函数,则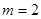 ;
;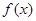 在
在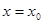 处有极值,则
处有极值,则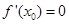 ”的否命题是真命题;
”的否命题是真命题;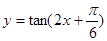 在区间
在区间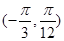 上单调递增;
上单调递增;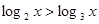 ”是“
”是“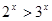 ”成立的充要条件。
”成立的充要条件。 a∈A∪B ②A
a∈A∪B ②A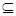 B
B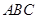 中,若
中,若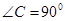 ,则
,则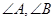 都是锐角”的否命题为 ;
都是锐角”的否命题为 ;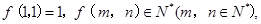 且对任何
且对任何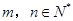 ,都有:
,都有: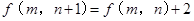 ,②
,②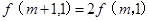 ,给出以下三个结论:(1)
,给出以下三个结论:(1)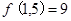 ;(2)
;(2)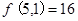 ;(3)
;(3)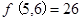 ,其中正确的是________.
,其中正确的是________.