题目内容
已知f(x)=ax2+bx+c的图象过原点(-1,0),是否存在常数a、b、c,使不等式x≤f(x) ≤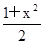 对一切实数x均成立?
对一切实数x均成立?
存在一组常数a= ,,b=
,,b= ,c=
,c=
解析试题分析:∵f(x)的图象过点(-1,0),∴a-b+c=0①
∵x≤f(x)≤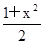 对一切x∈R均成立,
对一切x∈R均成立,
∴当x=1时也成立,即1≤a+b+c≤1.
故有a+b+c=1.②
由①②得b= ,c=
,c= -a.
-a.
∴f(x)=ax2+ x+
x+ -a≤
-a≤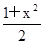 对一切x∈R成立,
对一切x∈R成立,
也即 恒成立?
恒成立? 即
即
解得a= .∴c=
.∴c= -a=
-a= .∴存在一组常数a=
.∴存在一组常数a= ,,b=
,,b= ,c=
,c= 使不等式x≤f(x) ≤
使不等式x≤f(x) ≤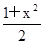 对一切实数x均成立
对一切实数x均成立
考点:本题主要考查函数恒成立问题;不等式的证明方法、二次函数的图象和性质。
点评:解答中赋值法(特殊值法)可以使“探索性”问题变得比较明朗,它是解决这类问题比较常用的方法。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 sinxcosx+2cos2x.
sinxcosx+2cos2x.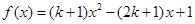 ,
, .
.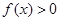 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 时,
时, 恒成立,求实数
恒成立,求实数 时,解不等式
时,解不等式
 (
( 为实数)有两个不相等的实数根,分别求:
为实数)有两个不相等的实数根,分别求: 的根为一正一负,则求实数
的根为一正一负,则求实数 内,则求实数
内,则求实数 (
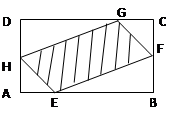
(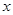 ,绿地面积为
,绿地面积为 .
.
 ,
, 是
是 的一个极值点.
的一个极值点.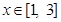 时,
时,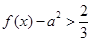 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.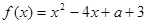 在区间
在区间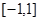 上存在零点;Q:函数
上存在零点;Q:函数 在
在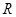 内没有极值点.若“P或Q”为真命题,“P且Q”为假命题,求实数
内没有极值点.若“P或Q”为真命题,“P且Q”为假命题,求实数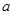 的取值范围.
的取值范围. ,
, ,使得
,使得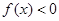 ,求实数
,求实数 的取值范围;
的取值范围; ,且
,且 在区间
在区间 上单调递增,求实数
上单调递增,求实数 ,若
,若 在
在 上的最大值为
上的最大值为 ,求
,求