题目内容
抛物线 上一点P到
上一点P到 轴的距离是4,则点P到该抛物线焦点的距离是( )
轴的距离是4,则点P到该抛物线焦点的距离是( )
| A.4 | B.6 | C.8 | D.12 |
B
解析试题分析:由方程可知准线为 ,P到
,P到 轴的距离是4,所以P到准线的距离为6,由抛物线定义可知P到该抛物线焦点的距离是6
轴的距离是4,所以P到准线的距离为6,由抛物线定义可知P到该抛物线焦点的距离是6
考点:抛物线的定义
点评:抛物线上的点到焦点的距离与其到准线的距离相等,利用这一点可实现两距离的转化

练习册系列答案
相关题目
双曲线 -
-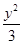 =1的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r=( )
=1的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r=( )
A. | B.2 | C.3 | D.6 |
下列曲线中,离心率为2的是( )
A. | B. | C. | D. |
抛物线 的焦点坐标是( )
的焦点坐标是( )
A. | B. | C.  | D. |
设抛物线y2 = 8x的准线与x轴交于点Q,若过点Q的直线 与抛物线有公共点,则直线
与抛物线有公共点,则直线 的斜率的取值范围是( )
的斜率的取值范围是( )
A.[- , , ] ] | B.[-2 , 2 ] | C.[-1 , 1 ] | D.[-4 , 4 ] |
过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有( )
| A.1条 | B.2条 | C.3条 | D.4条 |
等轴双曲线x2-y2=a2与直线y=ax(a>0)没有公共点,则a的取值范围( )
| A.a=1 | B.0<a<1 | C.a>1 | D.a≥1 |
 ,
, ),P2的柱坐标是P2(2,
),P2的柱坐标是P2(2, ,1),则|P1P2|=( )
,1),则|P1P2|=( )

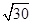

 的棱长为
的棱长为 ,点
,点 在棱
在棱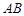 上, 且
上, 且 , 点
, 点 是平面
是平面 上的动点,且动点
上的动点,且动点 的距离与点
的距离与点