题目内容
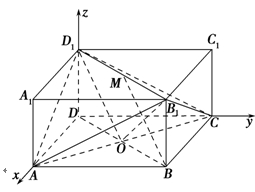
如图所示的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,O为AC与BD的交点,BB1=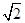 ,M是线段B1D1的中点.
,M是线段B1D1的中点.
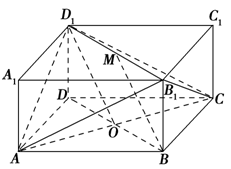
(1)求证:BM∥平面D1AC;
(2)求证:D1O⊥平面AB1C;
(3)求二面角B-AB1-C的大小.
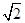 ,M是线段B1D1的中点.
,M是线段B1D1的中点.
(1)求证:BM∥平面D1AC;
(2)求证:D1O⊥平面AB1C;
(3)求二面角B-AB1-C的大小.
60°.
(1)证明 建立如图所示的空间直角坐标系,则点O(1,1,0)、D1(0,0,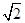 ),
),
∴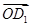 =(-1,-1,
=(-1,-1,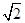 ),
),
又点B(2,2,0),M(1,1,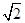 ),
),
∴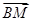 =(-1,-1,
=(-1,-1,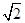 ),
),
∴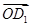 =
=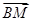 ,又∵OD1与BM不共线,
,又∵OD1与BM不共线,
∴OD1∥BM.
又OD1?平面D1AC,BM?平面D1AC,
∴BM∥平面D1AC.
(2)证明 连接OB1.∵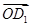 ·
·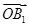 =(-1,-1,
=(-1,-1,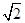 )·(1,1,
)·(1,1,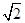 )=0,
)=0,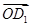 ·
·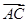 =
=
(-1,-1,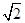 )·(-2,2,0)=0,∴
)·(-2,2,0)=0,∴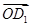 ⊥
⊥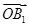 ,
,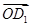 ⊥
⊥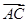 ,即OD1⊥OB1,OD1⊥AC,又OB1∩AC=O,∴D1O⊥平面AB1C.
,即OD1⊥OB1,OD1⊥AC,又OB1∩AC=O,∴D1O⊥平面AB1C.
(3)解 ∵CB⊥AB,CB⊥BB1,∴CB⊥平面ABB1,∴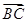 =(-2,0,0)为平面ABB1的一个法向量.由(2)知
=(-2,0,0)为平面ABB1的一个法向量.由(2)知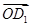 为平面AB1C的一个法向量.
为平面AB1C的一个法向量.
∴cos〈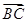 ,
,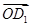 〉=
〉=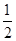 ,∴
,∴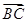 与
与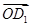 的夹角为60°,即二面角B-AB1-C的大小为60°.
的夹角为60°,即二面角B-AB1-C的大小为60°.
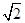 ),
),∴
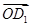 =(-1,-1,
=(-1,-1,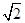 ),
),又点B(2,2,0),M(1,1,
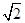 ),
),∴
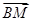 =(-1,-1,
=(-1,-1,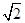 ),
),∴
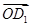 =
=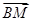 ,又∵OD1与BM不共线,
,又∵OD1与BM不共线,∴OD1∥BM.
又OD1?平面D1AC,BM?平面D1AC,
∴BM∥平面D1AC.

(2)证明 连接OB1.∵
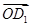 ·
·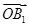 =(-1,-1,
=(-1,-1,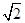 )·(1,1,
)·(1,1,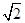 )=0,
)=0,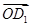 ·
·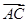 =
=(-1,-1,
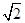 )·(-2,2,0)=0,∴
)·(-2,2,0)=0,∴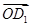 ⊥
⊥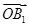 ,
,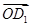 ⊥
⊥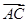 ,即OD1⊥OB1,OD1⊥AC,又OB1∩AC=O,∴D1O⊥平面AB1C.
,即OD1⊥OB1,OD1⊥AC,又OB1∩AC=O,∴D1O⊥平面AB1C.(3)解 ∵CB⊥AB,CB⊥BB1,∴CB⊥平面ABB1,∴
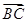 =(-2,0,0)为平面ABB1的一个法向量.由(2)知
=(-2,0,0)为平面ABB1的一个法向量.由(2)知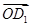 为平面AB1C的一个法向量.
为平面AB1C的一个法向量.∴cos〈
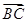 ,
,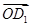 〉=
〉=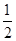 ,∴
,∴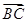 与
与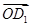 的夹角为60°,即二面角B-AB1-C的大小为60°.
的夹角为60°,即二面角B-AB1-C的大小为60°.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
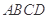 中,
中,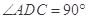 ,
,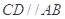 ,
,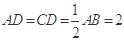 ,点
,点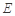 为
为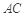 中点.将
中点.将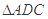 沿
沿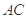 折起,使平面
折起,使平面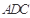
 平面
平面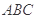 ,得到几何体
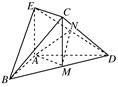
,得到几何体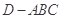 ,如图2所示.
,如图2所示.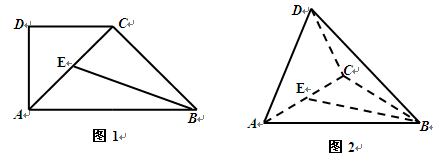
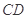 上找一点
上找一点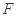 ,使
,使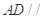 平面
平面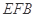 ;
; 到平面
到平面 的距离.
的距离. .
.
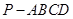 中,底面
中,底面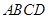 是矩形,四条侧棱长均相等且
是矩形,四条侧棱长均相等且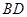 交
交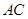 于点
于点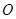 .
.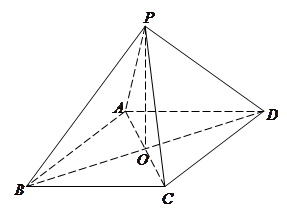
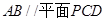 ;
;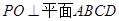 .
.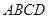 -
-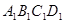 为正方体,下列结论错误的是( )
为正方体,下列结论错误的是( )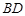 ∥
∥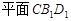
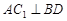
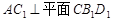
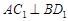
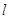 ⊥平面
⊥平面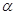 ,直线m
,直线m ,给出下列命题:
,给出下列命题: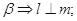 ②
②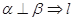 ∥m; ③
∥m; ③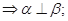 ④
④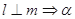 ∥
∥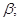 其中正确的命题是( )
其中正确的命题是( )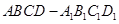 中,下列结论不正确的是 ( )
中,下列结论不正确的是 ( )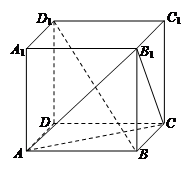
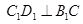
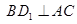
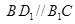
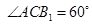
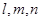 是三条互不相同的空间直线,
是三条互不相同的空间直线,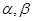 是两个不重合的平面,
是两个不重合的平面,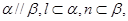 则
则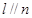 ; ②若
; ②若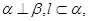 则
则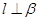 ;
;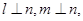 则
则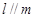 ; ④若
; ④若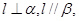 则
则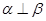
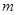 、
、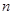 表示不同的直线,
表示不同的直线,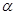 ,
,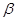 ,
,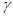 表示不同的平面,则下列四个命题正确的是 .
表示不同的平面,则下列四个命题正确的是 .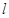 ,且
,且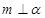 ,则
,则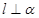 ;②若
;②若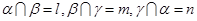 ,则
,则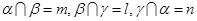 ,且
,且