题目内容
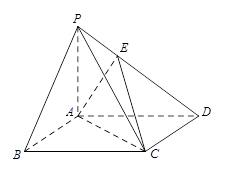
如图,在几何体ABCDE中,AB=AD=2,AB⊥AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,且AE=MC=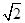 .
.
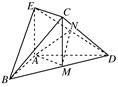
(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.
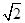 .
.
(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.
(1)见解析(2)见解析
(1)证明:∵AB=AD=2,AB⊥AD,M为线段BD的中点,
∴AM= BD=
BD=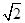 ,AM⊥BD,
,AM⊥BD,
∵AE=MC=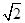 ,
,
∴AE=MC= BD=
BD=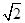 ,
,
∴BC⊥CD,BD⊥CM.
∵AE⊥平面ABD,MC∥AE,∴MC⊥平面ABD,
∴MC⊥AM,∴AM⊥平面CBD.
又MC∥AE,AE=MC=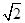 ,
,
∴四边形AMCE为平行四边形,∴EC∥AM,
∴EC⊥平面CBD,∴BC⊥EC,
∵EC∩CD=C,
∴BC⊥平面CDE.
∵BC?平面BCD,∴平面BCD⊥平面CDE.
(2)∵M为BD的中点,N为DE的中点,
∴MN∥BE.
由(1)知EC∥AM且AM∩MN=M,
又BE∩EC=E,
∴平面AMN∥平面BEC.
∴AM=
 BD=
BD=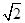 ,AM⊥BD,
,AM⊥BD,∵AE=MC=
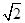 ,
,∴AE=MC=
 BD=
BD=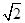 ,
,∴BC⊥CD,BD⊥CM.
∵AE⊥平面ABD,MC∥AE,∴MC⊥平面ABD,
∴MC⊥AM,∴AM⊥平面CBD.
又MC∥AE,AE=MC=
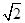 ,
,∴四边形AMCE为平行四边形,∴EC∥AM,
∴EC⊥平面CBD,∴BC⊥EC,
∵EC∩CD=C,
∴BC⊥平面CDE.
∵BC?平面BCD,∴平面BCD⊥平面CDE.
(2)∵M为BD的中点,N为DE的中点,
∴MN∥BE.
由(1)知EC∥AM且AM∩MN=M,
又BE∩EC=E,
∴平面AMN∥平面BEC.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
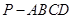 中,底面
中,底面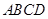 是正方形,
是正方形,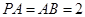 ,
,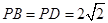 ,点
,点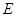 在
在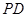 上,且
上,且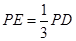 .
.
 平面
平面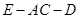 的余弦值;
的余弦值;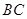 上存在点
上存在点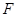 ,使
,使 ∥平面
∥平面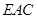 ,并求
,并求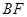 的长.
的长.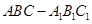 中,
中,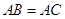 ,点
,点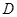 是
是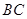 的中点。
的中点。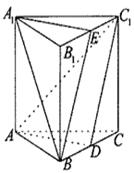
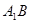 ∥平面
∥平面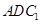
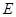 是
是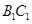 的中点,求证:平面
的中点,求证:平面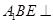 平面
平面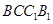 .
.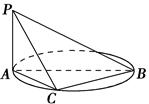
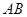 是圆
是圆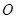 的直径,
的直径, 垂直圆
垂直圆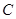 是圆
是圆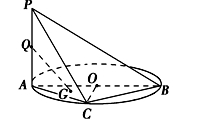
 平面
平面 ;
; 为
为 为
为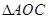 的重心,求证:
的重心,求证: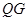 //平面
//平面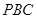 .
.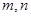 是两条不同的直线,
是两条不同的直线,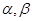 是两个不同的平面,给出下列条件,能得到
是两个不同的平面,给出下列条件,能得到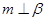 的是( )
的是( )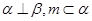
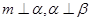
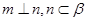
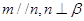
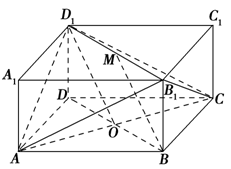
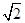 ,M是线段B1D1的中点.
,M是线段B1D1的中点.