题目内容
若向量
=（x，2x），
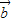=（-3x，2），且
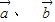的夹角为钝角，则x的取值范围是 ．
【答案】分析：本题考查的知识点是平面向量数量积表示两个向量的夹角，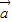
=（x，2x），
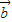=（-3x，2），且
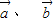的夹角为钝角，结合数量积表示两个向量的夹角，我们可以得到一个关于x的不等式，解不等式即可得到x的取值范围，但要注意，
与
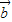反向的排除．
解答：解：∵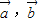
的夹角θ为钝角
又∵向量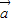
=（x，2x），
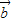=（-3x，2），
∴cosθ=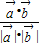
=
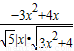＜0
即-3x2+4x＜0
解x＜0，或x＞
又∵当x=-
时，
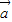与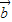
反向，不满足条件
故满足条件的x的取值范围是（-∞，-
）∪（-
，0）∪（
，+∝）
故答案为：（-∞，-
）∪（-
，0）∪（
，+∝）
点评：本题是一个易错题，容易只由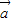
，
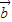的夹角为钝角得到
，而忽视了
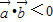不是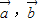
夹角为钝角的充要条件，因为
，
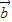的夹角为180°时也有
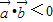，从而扩大x的范围，导致错误．
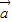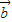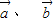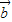=（x，2x），=（-3x，2），且的夹角为钝角，结合数量积表示两个向量的夹角，我们可以得到一个关于x的不等式，解不等式即可得到x的取值范围，但要注意，与反向的排除．解答：解：∵
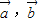的夹角θ为钝角又∵向量
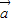=（x，2x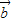），=（-3x，2），∴cosθ=
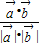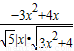=＜0即-3x2+4x＜0
解x＜0，或x＞
又∵当x=-
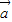时，与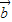反向，不满足条件故满足条件的x的取值范围是（-∞，-
）∪（-，0）∪（，+∝）故答案为：（-∞，-
）∪（-，0）∪（，+∝）点评：本题是一个易错题，容易只由
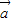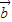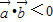，的夹角为钝角得到，而忽视了不是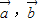夹角为钝角的充要条件，因为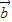，的夹角为180°时也有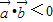，从而扩大x的范围，导致错误． 
练习册系列答案
相关题目