题目内容
设M、N为抛物线C:y=x2上的两个动点,过M、N分别作抛物线C的切线l1、l2,与x轴分别交于A、B两点,且l1与l2相交于点P,若|AB|=1.
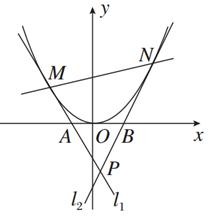
(1)求点P的轨迹方程;
(2)求证:△MNP的面积为一个定值,并求出这个定值.

(1)求点P的轨迹方程;
(2)求证:△MNP的面积为一个定值,并求出这个定值.
(1)y=x2-1 (2)见解析
(1)设M(m,m2),N(n,n2),则依题意知,切线l1,l2的方程分别为y=2mx-m2,y=2nx-n2,则A( ,0),B(
,0),B( ,0).
,0).
设P(x,y),由 ,得
,得 ①
①
因为|AB|=1,所以|n-m|=2,
即(m+n)2-4mn=4,将①代入上式,得
y=x2-1.
∴点P的轨迹方程为y=x2-1.
(2)证明:设直线MN的方程为y=kx+b(b>0).
联立方程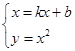
消去y,得x2-kx-b=0.
所以m+n=k,mn=-b.②
点P到直线MN的距离
d= ,
,
|MN|=|m-n|,
∴S△MNP= d·|MN|
d·|MN|
= |k(
|k( )-mn+b|·|m-n|
)-mn+b|·|m-n|
=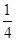 ·(m-n)2·|m-n|=2.
·(m-n)2·|m-n|=2.
即△MNP的面积为定值2.
 ,0),B(
,0),B( ,0).
,0).设P(x,y),由
 ,得
,得 ①
①因为|AB|=1,所以|n-m|=2,
即(m+n)2-4mn=4,将①代入上式,得
y=x2-1.
∴点P的轨迹方程为y=x2-1.
(2)证明:设直线MN的方程为y=kx+b(b>0).
联立方程
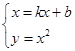
消去y,得x2-kx-b=0.
所以m+n=k,mn=-b.②
点P到直线MN的距离
d=
 ,
,|MN|=|m-n|,
∴S△MNP=
 d·|MN|
d·|MN|=
 |k(
|k( )-mn+b|·|m-n|
)-mn+b|·|m-n|=
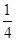 ·(m-n)2·|m-n|=2.
·(m-n)2·|m-n|=2.即△MNP的面积为定值2.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
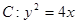 ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.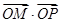 为定值;
为定值;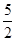 ,求向量
,求向量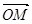 与
与 的夹角;
的夹角;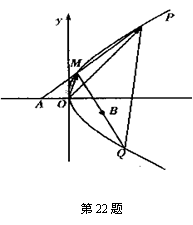

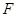 :
: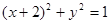 相内切,且与定直线
相内切,且与定直线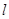 :
: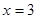 相切,则此动圆的圆心
相切,则此动圆的圆心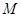 的轨迹方程是( )
的轨迹方程是( )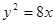
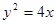
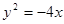
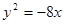
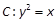 .命题p: 直线l1:
.命题p: 直线l1: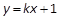 与抛物线C有公共点.命题q: 直线l2:
与抛物线C有公共点.命题q: 直线l2: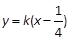 被抛物线C所截得的线段长大于2.若
被抛物线C所截得的线段长大于2.若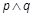 为假,
为假, 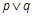 为真,求k的取值范围.
为真,求k的取值范围.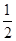 =0的距离等于( )
=0的距离等于( )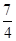 B.2 C.
B.2 C.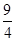 D.4
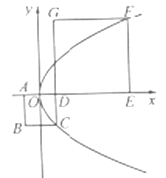
D.4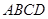 和正方形
和正方形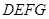 的边长分别为
的边长分别为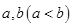 ,原点
,原点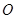 为
为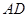 的中点,抛物线
的中点,抛物线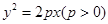 经过
经过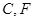 两点,则
两点,则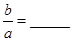 .
.
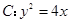 的焦点为
的焦点为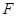 ,
,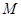 为抛物线
为抛物线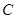 上一点,
上一点,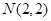 ,则
,则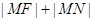 的取值范围是 .
的取值范围是 .