题目内容
【题目】在平面直角坐标系xOy中,圆O:![]() 与坐标轴分别交于A1,A2,B1,B2(如图).
与坐标轴分别交于A1,A2,B1,B2(如图).
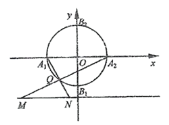
(1)点Q是圆O上除A1,A2外的任意点(如图1),直线A1Q,A2Q与直线![]() 交于不同的两点M,N,求线段MN长的最小值;
交于不同的两点M,N,求线段MN长的最小值;
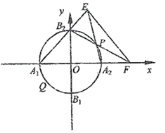
(2)点P是圆O上除A1,A2,B1,B2外的任意点(如图2),直线B2P交x轴于点F,直线A1B2交A2P于点E.设A2P的斜率为k,EF的斜率为m,求证:2m﹣k为定值.
(图1) (图2)
【答案】(1)2;(2)证明见解析。
【解析】
(1)设A2Q的斜率为k,求出直线A1Q和A2Q的方程,得出M,N的坐标,从而得出MN关于k的表达式,进而得出MN的最小值;
(2)求出直线方程,得出E、F的坐标,进而得出m与k的关系,从而得出结论.
(1)由题设可以得到直线![]() 的斜率存在设方程为
的斜率存在设方程为![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
由![]() ,解得
,解得 ;由
;由 ,解得
,解得![]()
所以,直线![]() 与直线
与直线![]() 的交点
的交点![]()
直线![]() 与直线
与直线![]() 的交点
的交点![]() ,所以
,所以![]() .
.
当![]() 时,
时, ![]() ,等号成立的条件是
,等号成立的条件是![]()
当![]() 时,
时, ![]() ,等号成立的条件是
,等号成立的条件是![]() .
.
故线段![]() 长的最小值是2.
长的最小值是2.
(2)法1:由题意可知![]() ,
,
![]() 的斜率为
的斜率为![]() ,∴直线
,∴直线![]() 的方程为
的方程为![]() ,由
,由![]() 得
得![]()
则直线![]() 的方程为
的方程为![]() ,令
,令![]() ,则
,则![]() ,即
,即![]()
∵直线![]() 的方程为
的方程为![]() ,由
,由![]() 解得
解得
∴![]() ,
,
∴![]() 的斜率
的斜率 ,
,
∴![]() (定值).
(定值).
法2:设![]() ,
, ![]() ,
,
![]() ,
,
所以![]() 直线方程:
直线方程: ![]()
![]() :直线方程
:直线方程![]() ,
,
则 ,得
,得![]()
而![]() ,得
,得![]()
![]() ,
,
则![]()
![]() (定值)。
(定值)。

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目

