Question

已知椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)的离心率为

3

2

，右焦点为F（c，0），P（x₀，y₀）是椭圆上一点，且x₀＞0，过P作圆x²+y²=b²的切线，交椭圆于另一点Q，设切点为M，
（1）用x₀表示|PM|；
（2）若△PQF的周长为16，求椭圆的方程．

Answer 1

分析：（1）将P（x₀，y₀）代入椭圆方程，结合椭圆的离心率为

3

2

化简得

y

2 0

=

1

4

a2-

1

4

x

2 0

，连结PO，OM，Rt△POM中利用勾股定理即可算出用x₀表示|PM|的式子；
（2）利用圆锥曲线的统一定义，算出|PF|=a-

3

2

x0，可得|PM|+|PF|=a，同理|QM|+|QF|=a．由此可得△PQF的周长为2a=16，从而得到a=8且b=4，可得椭圆的方程．

解答：解：（1）∵椭圆的离心率e=

c

a

=

3

2

，
∴c=

3

2

a，可得b2=

1

4

a2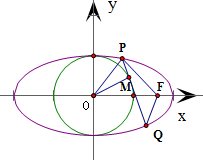
∵P（x₀，y₀）是椭圆上一点，
∴P坐标代入椭圆方程，化简得

y

2 0

=

1

4

a2-

1

4

x

2 0

，
连结PO，OM，可得OM⊥PQ
∴|PM|=

PO2-OM2

=

x 2 0 + y 2 0 -b2

=

3

2

x0…（6分）
（2）椭圆的右准线为x=

a2

c

即x=

2 3

3

a，
∴根据圆锥曲线统一定义，得

|PF|

2 3 3 a-x0

=

3

2

，
化简得|PF|=

3

2

(

2 3

3

a-x0)=a-

3

2

x0
∴|PM|+|PF|=a-

3

2

x0+

3

2

x 0=a，同理可得|QM|+|QF|=a
因此，|PQ|+|PF|+|QF|=（|PM|+|PF|）+（|QM|+|QF|）=2a=16，解得a=8，
由此可得b=

1

2

a=4，得椭圆的方程为 

x2

64

+

y2

16

=1．

点评：本题着重考查了椭圆的定义与标准方程、简单几何性质，考查了直线与圆的位置关系、勾股定理和圆锥曲线的统一定义等知识，属于中档题．