题目内容
用数学归纳法证明“ 时,从“
时,从“ 到
到 ”时,左边应增添的式子是( )
”时,左边应增添的式子是( )
A. | B. | C. | D. |

解析试题分析:当 时,等式的左边为
时,等式的左边为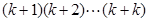 ;
;
当 时,等式的左边为
时,等式的左边为
对比可知:增加项为 .
.
考点:数学归纳法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
“若 ,则
,则 是函数
是函数 的极值点,因为
的极值点,因为 中,
中,  且
且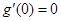 ,所以0是
,所以0是 的极值点.”在此“三段论”中,下列说法正确的是( )
的极值点.”在此“三段论”中,下列说法正确的是( )
| A.推理过程错误 | B.大前提错误 | C.小前提错误 | D.大、小前提错误 |
根据偶函数定义可推得“函数 在
在 上是偶函数”的推理过程是( )
上是偶函数”的推理过程是( )
| A.归纳推理 | B.类比推理 | C.演绎推理 | D.非以上答案 |
推理:因为平行四边形对边平行且相等,而矩形是特殊的平行四边形,所以矩形的对边平行且相等.以上推理的方法是( )
| A.合情推理 | B.演绎推理 | C.归纳推理 | D.类比推理 |
“所有金属都能导电,铁是金属,所以铁能导电,”此推理类型属于( )
| A.演绎推理 | B.类比推理 | C.合情推理 | D.归纳推理 |
用反证法证明命题“设 为实数,则方程
为实数,则方程 至少有一个实根”时,要做的假设是( )
至少有一个实根”时,要做的假设是( )
A.方程 没有实根 没有实根 | B.方程 至多有一个实根 至多有一个实根 |
C.方程 至多有两个实根 至多有两个实根 | D.方程 恰好有两个实根 恰好有两个实根 |

 在
在 方向上的投影.
方向上的投影. 
