题目内容

1．若等差数列{an}的前n项和为Sn，且S6=65，a7+a8+a9+a10+a11+a12=-15，则a13+a14+a15+a16+a17+a18=-95．

分析 由等差数列的性质可得S6，a7+a8+a9+a10+a11+a12，a13+a14+a15+a16+a17+a18成等差数列，结合已知数据可得答案．

解答 解：由等差数列的性质可得S6，a7+a8+a9+a10+a11+a12，a13+a14+a15+a16+a17+a18成等差数列，
∴a13+a14+a15+a16+a17+a18=2（a7+a8+a9+a10+a11+a12）-S6=-30-65=-95
故答案为：-95

点评 本题考查等差数列的性质，涉及“片段和”，属基础题．

练习册系列答案
相关题目
11．已知△ABC的三个内角A，B，C的对边分别是a，b，c，∠B=30°，（a-b）（a-2b）＜0，则△ABC解的情况是两解（填：一解、两解或无解）
12．圆C1的方程为（x-3）2+y2=$\frac{4}{25}$，圆C2的方程为（x-3-cosθ）2+（y-sinθ）2=$\frac{1}{25}$（θ∈R），过C2上任意一点P作圆C1的两条切线PM、PN，切点分别为M、N，则∠MPN的最大值为$\frac{π}{3}$．
9．（1）已知sinx+cosx=$\frac{1}{5}$，且$\frac{3π}{2}$＜x＜2π，求：sinx-cosx的值；
（2）求值：$sin{40°}（tan{10°}-\sqrt{3}）$．
16．函数f（x）=2x-x2（x∈[0，3]）的最大值M与最小值m的和等于（　　）
A．-1B．0C．1D．-2
6．设A=R，B=R，f：x→$\frac{2x+1}{2}$是A→B的映射．
（1）设3∈A，则3在B中的象是什么？
（2）设t∈A，且t在映射f下的象为5，则t应是多少？
（3）设s∈A，若s-1在映射f下的象为5，则s应是多少，s在映射f下的象是什么？
13．某学校高一年段共有480名学生，为了调查高一学生的学业水平，计划用系统抽样的方法抽取30名学生作为样本：将480名学生随机地从1～480编号，按编号顺序平均分成30组（1～16号，17～32号，…，465～480号），若从第1组中用抽签的方法确定的号码为5，则第8组中被抽中的学生的号码是117．
10．已知X是离散型随机变量，P（X=1）=$\frac{2}{3}$，P（X=a）=$\frac{1}{3}$，E（X）=$\frac{4}{3}$，则D（2X-1）等于（　　）
A．$\frac{8}{9}$B．-$\frac{1}{9}$C．$\frac{4}{3}$D．$\frac{1}{3}$
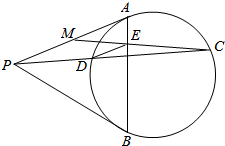11．如图，过圆外一点P分别作⊙O的两条切线PA，PB和一条割线PDC，记PA的中点为M，连接CM与AB交于点E．求证：DE∥PA．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网