题目内容
12.圆C1的方程为(x-3)2+y2=$\frac{4}{25}$,圆C2的方程为(x-3-cosθ)2+(y-sinθ)2=$\frac{1}{25}$(θ∈R),过C2上任意一点P作圆C1的两条切线PM、PN,切点分别为M、N,则∠MPN的最大值为$\frac{π}{3}$.分析 首先判断圆与圆的位置关系,进一步利用特殊位置把结论转化为解三角形问题,最后求出∠MPN的最大值.
解答 解:圆C1的方程为(x-3)2+y2=$\frac{4}{25}$,圆心坐标为:C1(3,0)半径r=$\frac{2}{5}$.
圆C2的方程(x-3-cosθ)2+(y-sinθ)2=$\frac{1}{25}$,圆心坐标为:C2(3+cosθ,sinθ),半径R=$\frac{1}{5}$.
由于cos2θ+sin2θ=1,|C1C2|>R+r,
所以两圆相离.
过C2上任意一点P作圆C1的两条切线PM、PN,切点分别为M、N,则要求∠MPN的最大值,
只需满足:在圆C2找到距离圆C1最近点即可.
所以|PC1|=1-$\frac{1}{5}$=$\frac{4}{5}$,|MC1|=$\frac{2}{5}$.
在Rt△MPC1中,根据|PC1|=$\frac{4}{5}$,|MC1|=$\frac{2}{5}$,解得:∠MPC1=$\frac{π}{6}$,
所以:∠MPN=$\frac{π}{3}$,
即∠MPN的最大值为:$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查的知识要点:圆与圆的位置关系,特殊位置出现相关的三角形知识,及角的最值问题.

练习册系列答案
相关题目
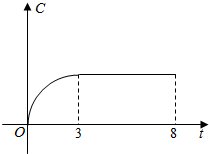 某工厂近8年来产品总量C与时间t(年)的关系如图所示,则下列说法中正确的序号是②③.
某工厂近8年来产品总量C与时间t(年)的关系如图所示,则下列说法中正确的序号是②③.