��Ŀ����
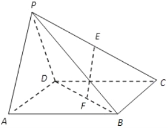
����Ŀ��һ�����̾����һ������OPQ��Ƥ����Բ�Ľǡ�POQ= ![]() ���뾶ΪR=200m�����������ڴ˵�Ƥ����һ��ƽ��ͼΪ���ε���ס¥��Ϊʹ�õ�Ƥ��ʹ�����������������Ʒ�����ͼ������һ������ABCD��һ��AB�ڰ뾶OP�ϣ�C��Բ���ϣ�D�ڰ뾶OQ��������������EFGH�Ķ�����Բ���ϣ�����G��H�ֱ��������뾶�ϣ�����ͨ�����㣬Ϊ�������ṩ���߽��飮
���뾶ΪR=200m�����������ڴ˵�Ƥ����һ��ƽ��ͼΪ���ε���ס¥��Ϊʹ�õ�Ƥ��ʹ�����������������Ʒ�����ͼ������һ������ABCD��һ��AB�ڰ뾶OP�ϣ�C��Բ���ϣ�D�ڰ뾶OQ��������������EFGH�Ķ�����Բ���ϣ�����G��H�ֱ��������뾶�ϣ�����ͨ�����㣬Ϊ�������ṩ���߽��飮 
���𰸡��⣺������һ����ͼ����OC���� ![]() ��
�� 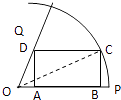
��Rt��OBC��BC=Rsinx��OB=Rcosx����DA=Rsinx
��Rt��OAD�� ![]() ����
���� ![]() ��
��
�� 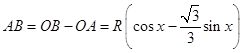 �������ABCD�����Ϊy����
�������ABCD�����Ϊy����
y=ABBC= 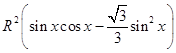 =
= ![]() sin��2x+
sin��2x+ ![]() ����
���� ![]() ��
��
�� ![]() ��
�� ![]() ��
��
���Ե� ![]() ����
���� ![]() ʱ
ʱ 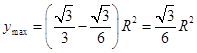 ��
��
������������ͼ����POQ��ƽ���߷ֱ�EF��GH�ڵ�M��N����OE��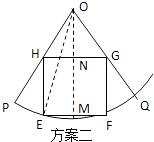
�� ![]() ����Rt��MOE��ME=Rsin����OM=Rcos��
����Rt��MOE��ME=Rsin����OM=Rcos��
��Rt��ONH�� ![]() ����
���� ![]() ��
��
�� ![]() �������EFGH�����ΪS��
�������EFGH�����ΪS��
��S=2MEMN=2R2sin����cos���� ![]() sin����=R2��sin2��+
sin����=R2��sin2��+ ![]() cos2����
cos2���� ![]() ��=
��= ![]()
�� ![]() ����
���� ![]() �����Ե�
�����Ե� ![]() ����
���� ![]() ʱ
ʱ ![]() ��
�� ![]() ����ymax��Smax
����ymax��Smax
�𣺸�������������߽��飺ѡ�÷���һ���ã�
���������������ۣ����շ���һ������Ҫ��������ۣ�
����һ����OC���� ![]() �������ABCD�����Ϊy����y=ABBC��ͨ�����뻯�������Ǻ�������ֵȷ�������������Եó��𰸣�������������POQ��ƽ���߷ֱ�EF��GH�ڵ�M��N����OE����
�������ABCD�����Ϊy����y=ABBC��ͨ�����뻯�������Ǻ�������ֵȷ�������������Եó��𰸣�������������POQ��ƽ���߷ֱ�EF��GH�ڵ�M��N����OE���� ![]() �������EFGH�����ΪS�����S��ʽ�ӣ������Ǻ��������������ֵ��
�������EFGH�����ΪS�����S��ʽ�ӣ������Ǻ��������������ֵ��
��Ƚ϶������ֵ�Ĵ�С��ѡ�����ֵ���ɵó��𰸣�

 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�����Ŀ��������Ⱥ�и���Ѫ�͵�����ռ�ı������£�
Ѫ�� | A | B | AB | O |
��Ѫ�͵�����ռ����(%) | 28 | 29 | 8 | 35 |
��֪ͬ��Ѫ�͵��˿�����Ѫ��O��Ѫ��������κ�һ��Ѫ�͵��ˣ�������ͬѪ�͵��˲��ܻ�����Ѫ��С����B��Ѫ����С������Ҫ��Ѫ���ʣ�
(1)����һ���ˣ���Ѫ�������С���ĸ����Ƕ��٣�
(2)����һ���ˣ���Ѫ�������С���ĸ����Ƕ��٣�