题目内容
【题目】《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,过
,过![]() 点分别作
点分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,则三棱锥
,则三棱锥![]() 的体积的最大值为__________.
的体积的最大值为__________.
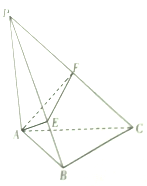
【答案】![]()
【解析】
由已知可得△AEF、△PEF均为直角三角形,且AF=2![]() ,由基本不等式可得当AE=EF=2时,△AEF的面积最大,然后由棱锥体积公式可求得体积最大值.
,由基本不等式可得当AE=EF=2时,△AEF的面积最大,然后由棱锥体积公式可求得体积最大值.
由PA⊥平面ABC,得PA⊥BC,
又AB⊥BC,且PA∩AB=A,∴BC⊥平面PAB,则BC⊥AE,
又PB⊥AE,则AE⊥平面PBC,
于是AE⊥EF,且AE⊥PC,结合条件AF⊥PC,得PC⊥平面AEF,
∴△AEF、△PEF均为直角三角形,由已知得AF=2![]() ,
,
而S△AEF=![]() (AE2+EF2)=
(AE2+EF2)=![]() AF2=2,
AF2=2,
当且仅当AE=EF=2时,取“=”,此时△AEF的面积最大,
三棱锥P﹣AEF的体积的最大值为:
VP﹣AEF=![]() =
=![]() =
=![]() .
.
故答案为:![]()

练习册系列答案
相关题目
