题目内容
已知椭圆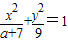
的离心率为
，则a= ．
【答案】分析：分类讨论椭圆的焦点和利用离心率计算公式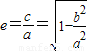
即可得出．
解答：解：①当a+7＞9，即a＞2时，椭圆的焦点在x轴上，∴e=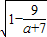
=
，解得a=5，满足条件；
②当a+7＜9，即a＜2时，椭圆的焦点在y轴上，∴e=
=
，解得a=-
，满足条件．
综上可知：a=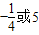
．
故答案为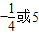
．
点评：熟练掌握分类讨论思想方法、椭圆的标准方程及其性质和离心率计算公式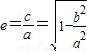
是解题的关键．
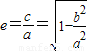即可得出．解答：解：①当a+7＞9，即a＞2时，椭圆的焦点在x轴上，∴e=
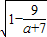=，解得a=5，满足条件；②当a+7＜9，即a＜2时，椭圆的焦点在y轴上，∴e=
=，解得a=-，满足条件．综上可知：a=
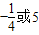．故答案为
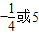．点评：熟练掌握分类讨论思想方法、椭圆的标准方程及其性质和离心率计算公式
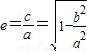是解题的关键． 
练习册系列答案
相关题目
已知椭圆的离心率为e，两焦点分别为F1、F2，抛物线C以F1为顶点、F2为焦点，点P为抛物线和椭圆的一个交点，若e|PF2|=|PF1|，则e的值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
，焦点是（-3，0），（3，0），则椭圆方程为（ ）
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在由圆O：x2+y2=1和椭圆C：
如图，A，B是椭圆C：