题目内容
2．利用矩阵解二元一次方程组：$\left\{\begin{array}{l}3x+y=2\\ 4x+2y=3\end{array}\right.$．分析 先根据系数行列式，得到矩阵A可逆．写出其逆矩阵，即可解得原方程组的解．
解答 解：方程组可写为$（{\begin{array}{l}3&1\\ 4&2\end{array}}）（\begin{array}{l}x\\ y\end{array}）=（\begin{array}{l}2\\ 3\end{array}）$，
系数行列式为3×2-4×1=2，方程组有唯一解．
利用矩阵求逆公式得${（{\begin{array}{l}3&1\\ 4&2\end{array}}）^{-1}}=（{\begin{array}{l}1&{-\frac{1}{2}}\\{-2}&{\frac{3}{2}}\end{array}}）$，
因此原方程组的解为$（\begin{array}{l}x\\ y\end{array}）=（{\begin{array}{l}1&{-\frac{1}{2}}\\{-2}&{\frac{3}{2}}\end{array}}）（\begin{array}{l}2\\ 3\end{array}）=（\begin{array}{l}\frac{1}{2}\\ \frac{1}{2}\end{array}）$，即$\left\{\begin{array}{l}x=\frac{1}{2}\\ y=\frac{1}{2}.\end{array}\right.$
点评 本小题主要考查逆变换与逆矩阵的计算、系数矩阵的逆矩阵解方程组等基础知识，考查运算求解能力与转化思想．属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
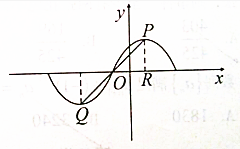已知函数f（x）=Acos（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜$\frac{π}{2}$），部分图象如图所示，PQ分别为图象的最高点和最低点，PR⊥x轴于R（$\frac{1}{2}$，0）点，∠RPQ=45°，|PQ|=2$\sqrt{2}$．