题目内容
已知椭圆 的左焦点为
的左焦点为 与过原点的直线相交于
与过原点的直线相交于 两点,连接
两点,连接 ,若
,若 ,则椭圆
,则椭圆 的离心率
的离心率
A. | B. | C. | D. |
A
解析试题分析:由已知条件,利用余弦定理求出|AF|,设F′为椭圆的右焦点,连接BF′,AF′.根据对称性可得四边形AFBF′是矩形,由此能求出离心率e.
考点:(1)余弦定理;(2)椭圆的几何性质.

练习册系列答案
相关题目
已知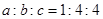 ,则双曲线
,则双曲线 的离心率为( )
的离心率为( )
A. | B.2 | C. | D. |
抛物线 的焦点到准线的距离是( )
的焦点到准线的距离是( )
| A.2 | B.1 | C. | D. |
已知双曲线的离心率为 ,且它有一个焦点与抛物线
,且它有一个焦点与抛物线 的焦点相同,那么双曲线的渐近线方程为( )
的焦点相同,那么双曲线的渐近线方程为( )
A. | B. | C. | D. |
已知直线 和直线
和直线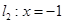 ,抛物线
,抛物线 上一动点
上一动点 到直线
到直线
和直线 的距离之和的最小值是( )
的距离之和的最小值是( )
A. | B.2 | C. | D.3 |
椭圆 中,以点
中,以点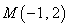 为中点的弦所在直线斜率为( )
为中点的弦所在直线斜率为( )
A. |
B. |
C. |
D. |
 的焦点F与椭圆
的焦点F与椭圆 的左焦点重合,点A在抛物线上,且
的左焦点重合,点A在抛物线上,且 ,若P是抛物线准线上一动点,则
,若P是抛物线准线上一动点,则 的最小值为( )
的最小值为( )


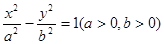 的左、右焦点分别为
的左、右焦点分别为 ,若
,若 为其上一点,且
为其上一点,且 ,
, ,则双曲线的离心率为( )
,则双曲线的离心率为( )



 ,定点
,定点 ,点
,点 为圆
为圆 上的动点,点
上的动点,点 在
在 上,点
上,点 在线段
在线段 上,且满足
上,且满足 ,则点
,则点


