题目内容
已知函数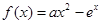
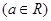 .
.
(1)当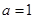 时,证明:
时,证明: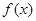 在
在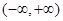 上为减函数;
上为减函数;
(2)若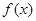 有两个极值点
有两个极值点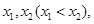 求实数
求实数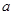 的取值范围.
的取值范围.
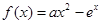
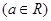 .
.(1)当
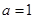 时,证明:
时,证明: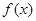 在
在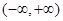 上为减函数;
上为减函数;(2)若
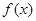 有两个极值点
有两个极值点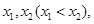 求实数
求实数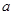 的取值范围.
的取值范围.(1)用导数来证明 (2)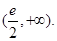
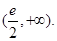
试题分析:(1)证明:
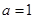 时,
时,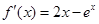 ,
,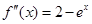 ,
,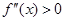 时,
时,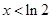 ;
;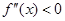 时,
时,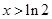 ;
;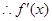 在区间
在区间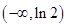 递增,在区间
递增,在区间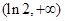 递减;
递减;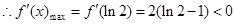 ,即
,即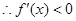 在
在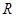 上恒成立,
上恒成立,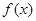 在
在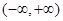 递减.
递减. (2)解:若
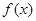 有两个极值点
有两个极值点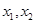 ,则
,则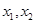 是方程
是方程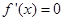 的两个根,故方程
的两个根,故方程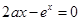 有两个根
有两个根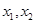 ,又
,又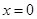 显然不是该方程的根,所以方程
显然不是该方程的根,所以方程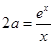 有两个根,
有两个根,设
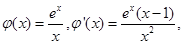 当
当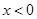 时,
时,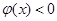 且
且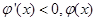 单调递减,
单调递减,当
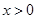 时,
时,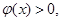 当
当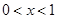 时,
时,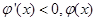 单调递减,当
单调递减,当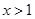 时,
时,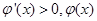 单调递增,要使方程
单调递增,要使方程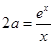 有两个根,需
有两个根,需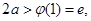 即
即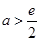 且
且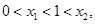 故
故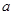 的取值范围为
的取值范围为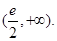
点评:本题考查了导数在解决函数极值和证明不等式中的应用,解题时要认真求导,防止错到起点,还要有数形结合的思想,提高解题速度.

练习册系列答案
相关题目
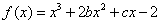 的图象在与
的图象在与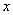 轴交点处的切线方程是
轴交点处的切线方程是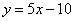 .
.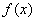 的解析式;
的解析式;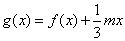 ,若
,若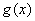 的极值存在,求实数
的极值存在,求实数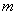 的取值范围以及当
的取值范围以及当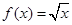 ,
,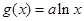 ,
,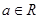
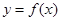 与曲线
与曲线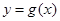 相交,且在交点处有相同的切线,求
相交,且在交点处有相同的切线,求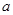 的值及该切线的方程;
的值及该切线的方程;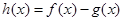 ,当
,当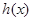 存在最小值时,求其最小值
存在最小值时,求其最小值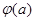 的解析式;
的解析式;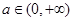 时,
时, 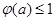 .
.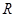 上的奇函数
上的奇函数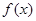 满足
满足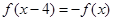 ,且在区间
,且在区间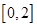 上是增函数,则当
上是增函数,则当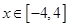 时,不等式
时,不等式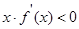 的解集为( )
的解集为( )

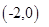

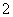 的等边三角形
的等边三角形 沿
沿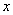 轴滚动,某时刻
轴滚动,某时刻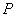 与坐标原点重合(如图),设顶点
与坐标原点重合(如图),设顶点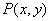 的轨迹方程是
的轨迹方程是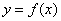 ,关于函数
,关于函数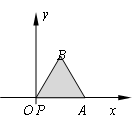
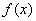 的值域为
的值域为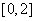 ;
;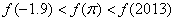 ;
;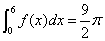 .
.
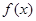 的图象如图所示,下列数值排序正确的是
的图象如图所示,下列数值排序正确的是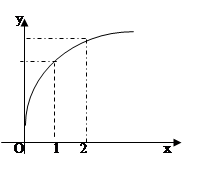

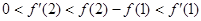

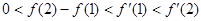
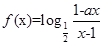 为奇函数,
为奇函数,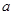 为常数,
为常数,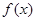 在区间
在区间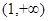 上单调递增;
上单调递增;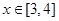 ,不等式
,不等式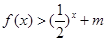 恒成立,求实数
恒成立,求实数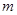 的取值范围。
的取值范围。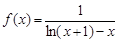 ,则
,则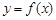 的大致图象是( )
的大致图象是( )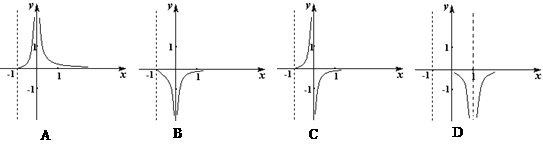
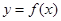 ,如果存在区间
,如果存在区间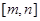 ,同时满足下列条件:①
,同时满足下列条件:①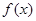 在
在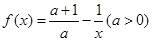 存在“梦想区间”,则
存在“梦想区间”,则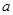 的取值范围是( )
的取值范围是( )