题目内容
设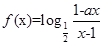 为奇函数,
为奇函数,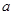 为常数,
为常数,
(1)求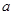 的值;
的值;
(2)证明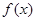 在区间
在区间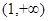 上单调递增;
上单调递增;
(3)若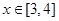 ,不等式
,不等式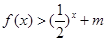 恒成立,求实数
恒成立,求实数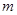 的取值范围。
的取值范围。
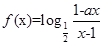 为奇函数,
为奇函数,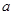 为常数,
为常数,(1)求
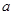 的值;
的值;(2)证明
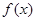 在区间
在区间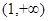 上单调递增;
上单调递增;(3)若
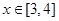 ,不等式
,不等式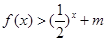 恒成立,求实数
恒成立,求实数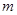 的取值范围。
的取值范围。(1)-1(2)∵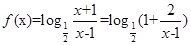 ,(
,(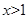 ),设
),设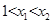 ,则
,则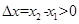
∵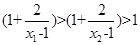 ,∴
,∴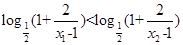 ∴
∴ ,
,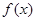 在区间
在区间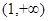 上单调递增(3)
上单调递增(3)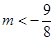
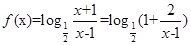 ,(
,(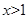 ),设
),设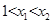 ,则
,则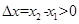
∵
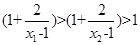 ,∴
,∴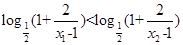 ∴
∴ ,
,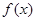 在区间
在区间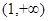 上单调递增(3)
上单调递增(3)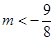
试题分析:(1)∵
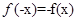 ,∴
,∴
∴
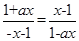 ,即
,即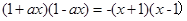 , ∴
, ∴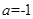
(2)∵
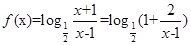 ,(
,(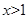 ),设
),设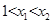 ,则
,则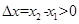
∵
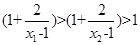 ,∴
,∴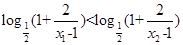
∴
 ,
,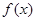 在区间
在区间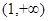 上单调递增
上单调递增(3)设
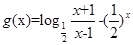 ,则
,则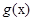 在
在 上是增函数
上是增函数∴
 对
对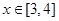 恒成立,∴
恒成立,∴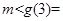 -
-
点评:若函数
 满足
满足 则是奇函数,若满足
则是奇函数,若满足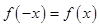 则是偶函数,第二问证明函数单调性采用的是定义的方法,此外导数法也是判定单调性常用方法,第三问不等式恒成立问题中常将其转化为求函数最值
则是偶函数,第二问证明函数单调性采用的是定义的方法,此外导数法也是判定单调性常用方法,第三问不等式恒成立问题中常将其转化为求函数最值
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
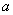 是实数.若函数
是实数.若函数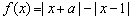 是定义在
是定义在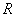 上的奇函数,但不是偶函数,则函数
上的奇函数,但不是偶函数,则函数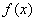 的递增区间为__________;
的递增区间为__________; 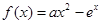
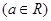 .
.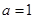 时,证明:
时,证明: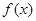 在
在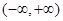 上为减函数;
上为减函数;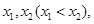 求实数
求实数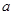 的取值范围.
的取值范围.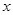 的不等式
的不等式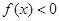 和
和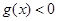 的解集分别为
的解集分别为 和
和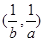 ,那么称这两个不等式为对偶不等式.如果不等式
,那么称这两个不等式为对偶不等式.如果不等式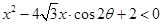 与不等式
与不等式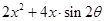
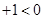 为对偶不等式,且
为对偶不等式,且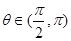 ,那么
,那么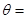 ______.
______.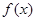 在定义域
在定义域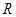 内可导,若
内可导,若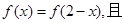
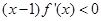 ,若
,若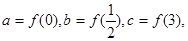 则
则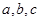 的大小关系是( )
的大小关系是( ) 
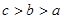
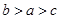

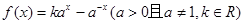 ,
,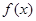 是定义域为R上的奇函数.
是定义域为R上的奇函数.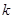 的值,并证明当
的值,并证明当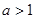 时,函数
时,函数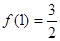 ,函数
,函数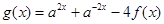 ,
,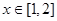 ,求
,求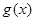 的值域;
的值域;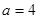 ,试问是否存在正整数
,试问是否存在正整数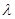 ,使得
,使得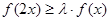 对
对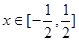 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数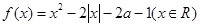 有四个不同的零点,则实数
有四个不同的零点,则实数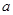 的取值范围是_______________.
的取值范围是_______________. 时,有不等式( )
时,有不等式( )
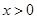 时
时 时
时