题目内容
【题目】已知抛物线y2=2x和圆x2+y2﹣x=0,倾斜角为 ![]() 的直线l经过抛物线的焦点,若直线l与抛物线和圆的交点自上而下依次为A,B,C,D,则|AB|+|CD|= .
的直线l经过抛物线的焦点,若直线l与抛物线和圆的交点自上而下依次为A,B,C,D,则|AB|+|CD|= .
【答案】3
【解析】解:由圆x2+y2﹣x=0,即(x﹣ ![]() )2+y2=
)2+y2= ![]() 可知,圆心为F(
可知,圆心为F( ![]() ,0),
,0),
半径为 ![]() ,抛物线y2=2x,得到抛物线焦点为F(
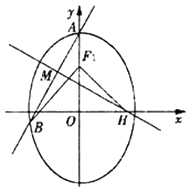
,抛物线y2=2x,得到抛物线焦点为F( ![]() ,0),如图:
,0),如图:
|AB|+|CD|=|AD|﹣|BC|
∵|BC|为已知圆的直径,∴|BC|=1,则|AB|+|CD|=|AD|﹣1.
设A(x1,y1)、D(x2,y2),
∵|AD|=|AF|+|FD|,而A、D在抛物线上,
由已知可知,直线l方程为y=x﹣ ![]() ,
,
由  消去y,得4x2﹣12x+1=0,
消去y,得4x2﹣12x+1=0,
∴x1+x2=3.∴|AD|=3+1=4,
因此,|AB|+|CD|=4﹣1=3.
所以答案是:3.


练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目